【题目】已知数轴上三点A,O,B表示的数分别为6,0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.
(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是 ;
(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?
(3)若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.

参考答案:
【答案】(1)1;(2)点P运动5秒时,追上点R;(3)线段MN的长度不发生变化,其长度为5.
【解析】试题分析:(1)由已知条件得到AB=10,由PA=PB,于是得到结论;
(2)设点P运动x秒时,在点C处追上点R,于是得到AC=6xBC=4x,AB=10,根据AC-BC=AB,列方程即可得到结论;
(3)线段MN的长度不发生变化,理由如下分两种情况:①当点P在A、B之间运动时②当点P运动到点B左侧时,求得线段MN的长度不发生变化.
试题解析:解:(1)(1)∵A,B表示的数分别为6,-4,
∴AB=10,
∵PA=PB,
∴点P表示的数是1,
(2)设点P运动x秒时,在点C处追上点R(如图)

则:AC=6x BC=4x AB=10
∵AC-BC=AB
∴ 6x-4x=10
解得,x=5
∴点P运动5秒时,追上点R.
(3)线段MN的长度不发生变化,理由如下:
![]()
分两种情况:
点P在A、B之间运动时:
MN=MP+NP=![]() AP+
AP+![]() BP=
BP=![]() (AP+BP)=
(AP+BP)=![]() AB=5
AB=5
点P运动到点B左侧时:
![]()
MN=MP-NP=![]() AP-
AP-![]() BP=
BP=![]() (AP-BP)=
(AP-BP)=![]() AB=5
AB=5
综上所述,线段MN的长度不发生变化,其长度为5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
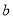 是最小的正整数,且
是最小的正整数,且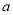 、
、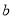 满足
满足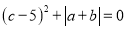 ,请回答问题:
,请回答问题:(
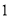 )请直接写出
)请直接写出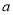 、
、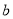 、
、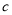 的值:
的值: 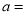 __________,
__________, 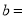 __________,
__________, 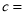 __________.
__________.(
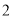 )数轴上
)数轴上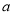 ,
, 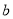 ,
, 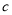 所对应的点分别为
所对应的点分别为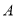 ,
, 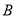 ,
, 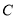 ,点
,点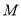 是
是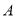 ,
, 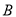 之间的一个动点,其对应的数为
之间的一个动点,其对应的数为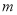 ,请化简
,请化简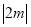 (请写出化简过程).
(请写出化简过程).(
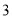 )在(
)在(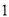 )、(
)、(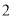 )的条件下,点
)的条件下,点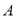 、
、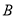 、
、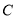 开始在数轴上运动,若点
开始在数轴上运动,若点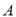 以每秒
以每秒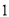 个单位长度的速度向左运动.同时,点
个单位长度的速度向左运动.同时,点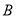 和点
和点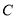 分别以每秒
分别以每秒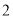 个单位长度和
个单位长度和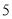 个单位长度的速度向右运动,假设
个单位长度的速度向右运动,假设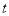 秒钟过后,若点
秒钟过后,若点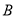 与点
与点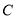 之间的距离表示为
之间的距离表示为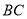 ,点
,点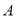 与点
与点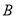 之间的距离表示为
之间的距离表示为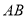 .请问:
.请问:  的值是否随着时间
的值是否随着时间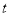 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:求1+2+22+23+24+…+22017的值.
解:设S=1+2+22+23+24+…+22017,
将等式两边同时乘以2得,2S=2+22+23+24+25+…+22017+22018,
将下式减去上式得:2S-S=22018-1,即S=22018-1,
所以1+2+22+23+24+…+2201722018-1,
请你依照此法计算:
(1)1+2+22+23+24+…+29;
(2)1+5+52+53+54+…+5n(其中n为正整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c经过A(-4,3)、B(2,0)两点,当x=3和x=-3时,这条抛物线上对应点的纵坐标相等.经过点C(0,-2)的直线l与 x轴平行,O为坐标原点.

(1)求直线AB和这条抛物线的解析式;
(2)以A为圆心,AO为半径的圆记为⊙A,判断直线l与⊙A的位置关系,并说明理由;
(3)设直线AB上的点D的横坐标为-1,P(m,n)是抛物线y=ax2+bx+c上的动点,当△PDO的周长最小时,求四边形CODP的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查瑞州市2016年初三年级学生的身高,从中抽取出200名学生进行调查,这个问题中样本容量为( )
A.被抽取的200名学生的身高
B.200
C.200名
D.初三年级学生的身高 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果 x2﹣kx﹣ab=(x﹣a)(x+b),则k应为( )
A.a﹣bB.a+bC.b﹣aD.﹣a﹣b
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年我市经济依然保持了平稳增长.据统计,截止到今年4月底,我市金融机构存款余额约为1193亿元,用科学记数法应记为元.
相关试题

