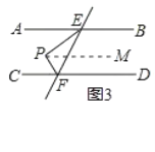
【题目】已知直线AB∥CD,直线EF与AB,CD分别相交于点E,F.

(1)如图1,若∠1=60°,求∠2=__________;∠3=__________.
(2)若点P是平面内的一个动点,连结PE,PF,探索∠EPF,∠PEB,∠PFD三个角之间的关系.
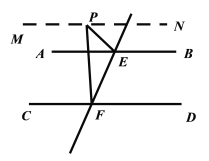
①当点P在图2的位置时,可得∠EPF=∠PEB+∠PFD. 理由如下:
如图2,过点P作MN∥AB,则∠EPM=∠PEB(__________)
∵AB∥CD(已知) MN∥AB(作图)
∴MN∥CD(__________)
∴∠MPF=∠PFD (__________)
∴__________+__________=∠PEB+∠PFD(等式的性质)
即:∠EPF=∠PEB+∠PFD.请补充完整说理过程(填写理由或数学式)
②当点P在图3的位置时,此时∠EPF=80°,∠PEB=156°,则∠PFD=__________;
③当点P在图4的位置时,写出∠EPF,∠PEB,∠PFD三个角之间的关系并证明(每一步必须注明理由).
参考答案:
【答案】(1)∠2=60°;∠3=60°;(2)①两直线平行,内错角相等;如果两条直线都和第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等;∠EPM+∠FPM;②124°;③∠EPF+∠PFD=∠PEB;证明见解析
【解析】
(1)根据对顶角相等求∠2,根据两直线平行,同位角相等求∠3;
(2)①过点P作MN//AB,根据平行线的性质得∠EPM=∠PEB,且有MN//CD,所以∠MPF=∠PFD,然后利用等式性质易得∠EPF=∠PEB十∠PFD;
②同①;
③利用平行线的性质和三角形的外角性质得到三个角之间的关系.
解:(1)应填∠2=60°,∠3=60°.理由是:
∵∠2=∠1,∠1=60°,
∴∠2=60°,
∵AB//CD
∴∠3=∠1=60°;
(2)①当点P在图(2)的位置时,可得∠EPF=∠PEB+∠PFD. 理由如下:
如图2,过点P作MN∥AB,则∠EPM=∠PEB(两直线平行,内错角相等)
∵AB∥CD(已知),MN∥AB(作图)
∴MN∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠MPF=∠PFD (两直线平行,内错角相等)
∴ ∠EPM+∠FPM =∠PEB+∠PFD(等式的性质)
即:∠EPF=∠PEB+∠PFD
故答案为:两直线平行,内错角相等;如果两条直线都和第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等;∠EPM+∠MP
②当点P在图3的位置时,此时∠EPF=80°,∠PEB=156°,则∠PFD=124°.理由为:
如图3所示,过点P作PM∥AB,
则∠PEB+∠EPM=180°,∠MPF+∠PFD=180°,
∴∠PEB+∠EPM+∠MPF+∠PFD=180°+180°=360°,即∠EPF+∠PEB+∠PFD=360°
∴∠PFD=360°-80°-156°=124°;
故答案为:124°
③当点P在图4的位置时,∠EPF,∠PEB,∠PFD三个角之间关系是:
∠EPF+∠PFD=∠PEB
证明如下:
如图4,过点P作MN∥AB,则∠EPM=∠PEB(两直线平行,内错角相等)
∵AB∥CD(已知),MN∥AB,
∴MN∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠MPF=∠PFD(两直线平行,内错角相等)
∴∠EPM-∠MPF=∠PEB-∠PFD(等式的性质)
即∠EPF+∠PFD=∠PEB
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在Rt△ABC中,∠C=90°,BC=6cm,AC=8 cm,AB=10 cm. 现有一动点P,从A点出发,沿着三角形的边AC-CB-BA运动,回到A点停止,速度为1 cm/s,设运动时间为t s.
(1)当t=_______时,△ABC的周长被线段AP平分为相等的两部分.
(2)当t=_______时,△APC的面积等于△ABC面积的一半.
(3)还有一个△DEF,∠E=90°,如图②所示,DE=4cm,DF=5cm,∠D=∠A. 在△ABC的边上,若另外有一个动点Q,与P 同时从A点出发,沿着边AB-BC-CA运动,回到点A停止. 在两点运动过程中某一时刻,恰好△APQ与△DEF全等,则点Q的运动速度 cm/s.


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一边长为2,周长为8,那么它的腰长为 ( )
A. 2 B. 3 C. 2或3 D. 不能确定
-
科目: 来源: 题型:
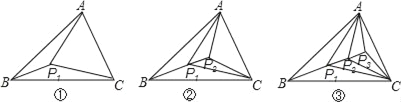
查看答案和解析>>【题目】如图,△ABC的三个顶点和它内部的点P1,把△ABC分成3个互不重叠的小三角形;△ABC的三个顶点和它内部的点P1、P2,把△ABC分成5个互不重叠的小三角形;△ABC的三个顶点和它内部的点 P1、P2、P3,把△ABC分成7个互不重叠的小三角形;…△ABC的三个顶点和它内部的点 P1、P2、P3、…、P2017,把△ABC分成_____个互不重叠的小三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点A,O,B表示的数分别为6,0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.
(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是 ;
(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?
(3)若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】股民李金上星期六买进某公司的股票,每股
 元,下表为本周内该股票的涨跌情况:
元,下表为本周内该股票的涨跌情况:星期
一
二
三
四
五
六
每股涨跌(与前一天相比)
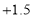
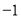
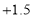
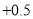
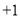
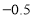
星期三收盘时,每股是________元;本周内最高价是每股________元, 最低价是每股______元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只小虫子落在数轴上的某点
 ,第一次从
,第一次从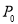 向左跳一个单位到
向左跳一个单位到 ,第二次从
,第二次从 向右跳
向右跳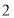 个单位到
个单位到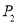 ,第三次从
,第三次从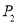 向左跳
向左跳 个单位到
个单位到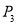 ,第四次从
,第四次从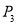 向右跳
向右跳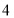 个单位到
个单位到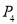 ,按以上规律跳了
,按以上规律跳了 次时,它落在数轴上的点
次时,它落在数轴上的点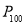 所表示的数恰好是2019,则这只小虫的初始位置
所表示的数恰好是2019,则这只小虫的初始位置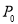 所在的数是_____.
所在的数是_____.
相关试题

