【题目】如图,在等边三角形ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=![]() ,则△ABC的边长为____.
,则△ABC的边长为____.

参考答案:
【答案】3
【解析】
根据等边三角形性质求出AB=BC=AC,∠B=∠C=60°,推出∠BAP=∠DPC,证△BAP∽△CPD,得出![]() ,代入求出即可.
,代入求出即可.
∵△ABC是等边三角形,
∴AB=BC=AC,∠B=∠C=60°,
∴∠BAP+∠APB=180°-60°=120°,
∵∠APD=60°,
∴∠APB+∠DPC=180°-60°=120°,
∴∠BAP=∠DPC,
即∠B=∠C,∠BAP=∠DPC,
∴△BAP∽△CPD,
∴![]() ,
,
∵CD=![]() ,CP=BC-BP=x-1,BP=1,
,CP=BC-BP=x-1,BP=1,
即![]() ,
,
解得:AB=3.
故答案为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交车每天的支出费用为600元,每天的乘车人数x(人)与每天利润(利润=票款收入﹣支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变):
x(人)
…
200
250
300
350
400
…
Y(元)
…
﹣200
﹣100
0
100
200
…
根据表格中的数据,回答下列问题:
(1)在这个变化关系中,自变量是什么?因变量是什么?
(2)若要不亏本,该公交车每天乘客人数至少达到多少?
(3)请你判断一天乘客人数为500人时,利润是多少?
(4)试写出该公交车每天利润y(元)与每天乘车人数x(人)的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB,垂足为D,E是AC边上一点,EH⊥AB,垂足为H,∠1=∠2.
(1)试说明DF∥AC;
(2)若∠A=38°,∠BCD=45°,求∠3的度数.

-
科目: 来源: 题型:
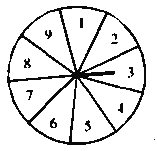
查看答案和解析>>【题目】如图,一个均匀的转盘被平均分成9等份,分别标有1,2,3,4,5,6,7,8,9这9个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字.
小亮和小芳两人玩转盘游戏,对游戏规则,小芳提议:若转岀的数字是3的倍数,小芳获胜,若转出的数字是4的倍数,小亮获胜.
(1)你认为小芳的提议合理吗?为什么?
(2)利用这个转盘,请你为他俩设计一种对两人都公平的游戏规则.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC(如图).
(1)利用尺规按下列要求作图(保留作图痕迹,不写作法):
①作∠BAC的平分线AD,交BC于点D;
②作AB边的垂直平分线EF,分别交AD,AB于点E,F.
(2)连接BE,若∠ABC=60°,∠C=40°,求∠AEB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,相交两圆的公共弦AB长为120cm,它分别是一圆内接正六边形的边和另一圆内接正方形的边,求两圆相交弧间的阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB,垂足为D,E是AC边上一点,EH⊥AB,垂足为H,∠1=∠2.
(1)试说明DF∥AC;
(2)若∠A=38°,∠BCD=45°,求∠3的度数.

相关试题

