【题目】如图,相交两圆的公共弦AB长为120cm,它分别是一圆内接正六边形的边和另一圆内接正方形的边,求两圆相交弧间的阴影部分的面积.

参考答案:
【答案】4200π﹣3600﹣3600![]()
【解析】试题分析:
如图,连接O1O2 , O1A,O1B,O2A,O2B,则可得O1O2垂直平分AB,由题意可得AC=BC=60,∠AO1B=60°,∠AO2B=90°,由此可得△AO1B是等边三角形,△AO2B是等腰直角三角形,再由S阴影=S扇形AO1B+S扇形AO2B-S△AO1B -S△AO2B,即可求得所求面积.
试题解析:
如图,连接O1O2 , O1A,O1B,O2A,O2B;
则O1O2垂直平分AB,
∵AB=120,
∴AC=BC=60;
由题意得:∠AO1B=![]() ,∠AO2B=90°,
,∠AO2B=90°,
又∵O1A=O1B,O2A=O2B,
∴△O1AB,△O2AB分别是等边三角形和等腰直角三角形,
∴O1A=AB=120,O2C=AC=60,O2A=![]() O2C=
O2C=![]()
∴S扇形AO1B=![]() ,S扇形AO2B=
,S扇形AO2B=![]() ,
,
S△AO1B=![]() ,S△AO2B=
,S△AO2B=![]() ,
,
∴S阴影=S扇形AO1B+S扇形AO2B-S△AO1B -S△AO2B
=![]()
=![]() (cm2).
(cm2).

-
科目: 来源: 题型:
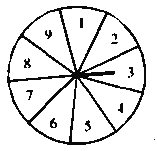
查看答案和解析>>【题目】如图,一个均匀的转盘被平均分成9等份,分别标有1,2,3,4,5,6,7,8,9这9个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字.
小亮和小芳两人玩转盘游戏,对游戏规则,小芳提议:若转岀的数字是3的倍数,小芳获胜,若转出的数字是4的倍数,小亮获胜.
(1)你认为小芳的提议合理吗?为什么?
(2)利用这个转盘,请你为他俩设计一种对两人都公平的游戏规则.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=
 ,则△ABC的边长为____.
,则△ABC的边长为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC(如图).
(1)利用尺规按下列要求作图(保留作图痕迹,不写作法):
①作∠BAC的平分线AD,交BC于点D;
②作AB边的垂直平分线EF,分别交AD,AB于点E,F.
(2)连接BE,若∠ABC=60°,∠C=40°,求∠AEB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB,垂足为D,E是AC边上一点,EH⊥AB,垂足为H,∠1=∠2.
(1)试说明DF∥AC;
(2)若∠A=38°,∠BCD=45°,求∠3的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣2x﹣3与x轴交于A、B两点(A在B的左边),与y轴交于点C.
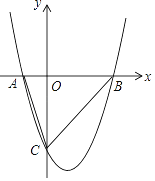
(1)求出点A、B、C的坐标.
(2)求S△ABC
(3)在抛物线上(除点C外),是否存在点N,使得S△NAB=S△ABC , 若存在,求出点N的坐标,若不 存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分别直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图
(2)求扇形统计图中m的值和E组对应的圆心角度数
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数
相关试题

