【题目】数学活动课上,某学习小组对有一内角(∠BAD)为120°的平行四边形ABCD,将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究:在(2)的条件下,学习小组某成员探究发现AE+2AF= ![]() AC,试判断结论是否正确,并说明理由.
AC,试判断结论是否正确,并说明理由.
参考答案:
【答案】
(1)
①证明:如图1中,
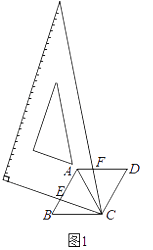
∵四边形ABCD 是平行四边形,∠BAD=120°,
∴∠D=∠B=60°,
∵AD=AB,
∴△ABC,△ACD都是等边三角形,
∴∠B=∠CAD=60°,∠ACB=60°,BC=AC,
∵∠BCF=60°,
∴∠BCE+∠ACE=∠ACF+∠ACE=60°,
∴∠BCE=∠ACF,
在△BCE和△ACF中,
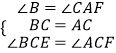 ,
,
∴△BCE≌△ACF.
②如图1中,
∵△BCE≌△ACF,
∴BE=AF,
∴AE+AF=AE+BE=AB=AC.
∴AE+AF=AC.
(2)
证明:如图2中,
设DH=x,由题意CD=2x,CH= ![]() x.
x.
∴AD=2AB=4x,AH=AD﹣DH=3x,
∵CH⊥AD,
∴AC= ![]() =2
=2 ![]() x,
x,
∴AC2+CD2=16x2,AD2=16x2,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴∠BAC=∠ACD=90°,
∴∠CAD=30°,
∴∠ACH=60°,
∵∠ECF=60°=∠ACH,
∴∠HCF=∠ACE,
∴△ACE∽△HCF,
∴ ![]() =
= ![]() =2,
=2,
∴AE=2FH.
(3)
结论正确.
理由:如图2中,由(2)可知,设FH=α,则AE=2a,设AH=x,则AH=3x,
易知AC=2 ![]() x,
x,
∴AF=3x﹣a,
∴AE+2AF=2a+2(3x﹣a)=6x= ![]() AC.
AC.
【解析】(1)①首先证明△ABC,△ACD都是等边三角形,根据ASA即可证明.②利用①中结论,即可证明.(2)首先利用勾股定理逆定理证明△ACD是直角三角形,再证明△ACE∽△HCF,即可推出 ![]() =
= ![]() =2.(3)利用代数法证明,如图2中,由(2)可知,设FH=α,则AE=2a,设AH=x,则AH=3x,易知AC=2
=2.(3)利用代数法证明,如图2中,由(2)可知,设FH=α,则AE=2a,设AH=x,则AH=3x,易知AC=2 ![]() x,AF=3x﹣a,即可得出AE+2AF=2a+2(3x﹣a)=6x=
x,AF=3x﹣a,即可得出AE+2AF=2a+2(3x﹣a)=6x= ![]() AC.
AC.
【考点精析】关于本题考查的相似三角形的应用,需要了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能得出正确答案.
-
科目: 来源: 题型:
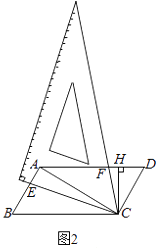
查看答案和解析>>【题目】(如图(1),一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在线段OP上滑动,将窗户OM按图示方向向内旋转45°到达ON位置,如图(2),此时,点A、C的对应位置分别是点B、D,测量出∠ODB为37°,点D到点O的距离为28cm.
(1)求B点到OP的距离.
(2)求滑动支架AC的长. (参考数据:sin37°=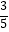 ,cos37°=
,cos37°= 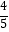 ,tan37°=
,tan37°=  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】新化到长沙的距离约为200km,小王开着小轿车,张师傅开着大货车都从新化去长沙,小王比张师傅晚出发20分钟,最后两车同时到达长沙.已知小轿车的速度是大货车速度的1.2倍,求小轿车和大货车的速度各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的边AB为直径作⊙O,交边BC于点D,点E是
 上一点.
上一点. 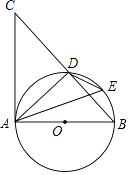
(1)若AC为⊙O的切线,试说明:∠AED=∠CAD;
(2)若AE平分∠BAD,延长DE、AB交于点P,若PB=BO,DE=2,求PD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一架飞机在两城之间飞行,风速为24千米/小时,顺风飞行需2小时50分,逆风飞行需要3小时.
(1)求无风时飞机的飞行速度;
(2)求两城之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,已知△ABC 中,其中 A(0,﹣2),B(2,﹣4),C(4,﹣1).
(1)画出与△ABC 关于 y 轴对称的图形△A1B1C1;
(2)写出△A1B1C1 各顶点坐标;
(3)求△ABC 的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣6x+c与x轴交于点A、B(5,0),与y轴交于点C(0,5),点P是抛物线上的动点,设点P的横坐标为t,连接PB、PC,PC与x轴交于点D,过点P作y轴的平行线交x轴于点H、交直线BC于点E.
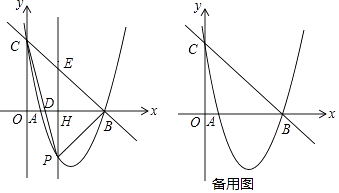
(1)求该抛物线所对应的函数解析式;
(2)若点P在第四象限,则△BPC的面积有值(填“最大”或“最小”),并求出其值;
(3)当t<5时,△BPE能否为等腰三角形?若能,请求出此时点P的坐标;若不能,请说明理由.
相关试题

