【题目】一架飞机在两城之间飞行,风速为24千米/小时,顺风飞行需2小时50分,逆风飞行需要3小时.
(1)求无风时飞机的飞行速度;
(2)求两城之间的距离.
参考答案:
【答案】(1)无风时飞机的飞行速度为840千米每小时;(2)两城之间的距离为2448千米.
【解析】
应先设出飞机在无风时的速度为x,从而可知在顺风时的速度为飞机在无风中的速度加上风速,飞机在逆风中的速度等于飞机在无风中的速度减去风速,又已知了顺风飞行和逆风飞行所用的时间,再根据路程相等,列出等式,求解即可.
(1)设无风时飞机的速度为x千米每小时,两城之间的距离为S千米
则顺风飞行时的速度v1=x+24,逆风飞行的速度v2=x﹣24
顺风飞行时:S=v1t1
逆风飞行时:S=v2t2
即S=(x+24)×2![]() =(x﹣24)×3
=(x﹣24)×3
解得x=840,
答:无风时飞机的飞行速度为840千米每小时.
(2)两城之间的距离S=(x﹣24)×3=2448千米
答:两城之间的距离为2448千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新化到长沙的距离约为200km,小王开着小轿车,张师傅开着大货车都从新化去长沙,小王比张师傅晚出发20分钟,最后两车同时到达长沙.已知小轿车的速度是大货车速度的1.2倍,求小轿车和大货车的速度各是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的边AB为直径作⊙O,交边BC于点D,点E是
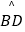 上一点.
上一点. 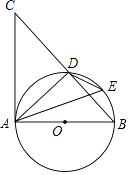
(1)若AC为⊙O的切线,试说明:∠AED=∠CAD;
(2)若AE平分∠BAD,延长DE、AB交于点P,若PB=BO,DE=2,求PD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,某学习小组对有一内角(∠BAD)为120°的平行四边形ABCD,将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究:在(2)的条件下,学习小组某成员探究发现AE+2AF=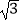 AC,试判断结论是否正确,并说明理由.
AC,试判断结论是否正确,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,已知△ABC 中,其中 A(0,﹣2),B(2,﹣4),C(4,﹣1).
(1)画出与△ABC 关于 y 轴对称的图形△A1B1C1;
(2)写出△A1B1C1 各顶点坐标;
(3)求△ABC 的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2﹣6x+c与x轴交于点A、B(5,0),与y轴交于点C(0,5),点P是抛物线上的动点,设点P的横坐标为t,连接PB、PC,PC与x轴交于点D,过点P作y轴的平行线交x轴于点H、交直线BC于点E.
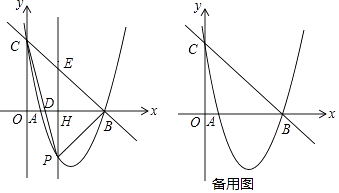
(1)求该抛物线所对应的函数解析式;
(2)若点P在第四象限,则△BPC的面积有值(填“最大”或“最小”),并求出其值;
(3)当t<5时,△BPE能否为等腰三角形?若能,请求出此时点P的坐标;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的内容,再解决问题,
例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0
∴m=﹣3,n=3
问题(1)若x2+2y2﹣2xy+4y+4=0,求xy的值.
(2)已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c是△ABC中最长的边,求c的取值范围.
相关试题

