【题目】解方程组:
(1)![]() (代入法)
(代入法)
(2)![]() (加减法)
(加减法)
(3)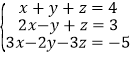
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)
【解析】
(1)把第二个方程用含有y的字母把x表示出来 ,然后代入第一个方程求出y,再把y代入求出x,方程组的解即可求出
(2)把第一个方程左右两边都乘以2,第二个方程左右两边都乘以3,然后相减消掉y求出x,然后把x代入求出y,方程组的解即可求出.
(3)先把三元一次方程组转换成二元一次方程组,然后求解即可
(1)解:![]() , 由②得x=13﹣4y ③,
, 由②得x=13﹣4y ③,
将③代入①得2(13﹣4y)+3y=16,解得:y=2,
将y=2代入②得:x=5,
∴原方程组的解为![]()
(2)解:用加减消元法求解:![]() ,
,
①×2得:10x﹣12y=﹣6 ③
②×3得:21x﹣12y=27④
④﹣③得:21x﹣12y﹣10x+12y=33,解得:x=3,
将x=3代入①得:y=3,
∴原方程组的解为![]()
(3)解: , ②﹣①得:x﹣2y=﹣1 ④
, ②﹣①得:x﹣2y=﹣1 ④
①×3得,3x+3y+3z=12 ⑤
⑤+③得6x+y=7 ⑥
⑥×2,得:12x+2y=14 ⑦
⑦+④得13x=13,解得:x=1,
将x=1代入④得y=1,
将x=1、y=1代入①得z=2,
∴原方程组的解为
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读探索
知识累计
解方程组
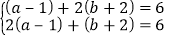
解:设a﹣1=x,b+2=y,原方程组可变为

解方程组得:
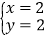 即
即 所以
所以 此种解方程组的方法叫换元法.
此种解方程组的方法叫换元法.(1)拓展提高
运用上述方法解下列方程组:

(2)能力运用
已知关于x,y的方程组
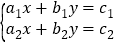 的解为
的解为 ,直接写出关于m、n的方程组
,直接写出关于m、n的方程组 的解为_____________.
的解为_____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明到某服装专卖店去做社会调查,了解到该专卖店为了微励营业员的工作积极性,实行“月总收入=基本工资(固定)+计付奖金”的方法计算薪资,并获得如下信息;
营业员
小张
小王
月销售件数
200
150
月总收入/元
1400
1250
销售每件奖励a元,晋业员月基本工资为b元.
(1)列方程组求a,b的值.
(2)假设月销售件数为x,月总收入为y元,请写出y与x的函数关系式,并求出营业员小张上个月总收入是1700元时,小张上个月卖了多少件服装?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2i=﹣i,i4=(i2)2=(﹣1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4ni=i,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1.
计算:(1)i.i2.i3.i4
(2)i+i2+i3+i4+…+i2017+i2018. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.

完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“两直线平行,内错角的平分线互相平行”是真命题吗?如果是,请给出证明;如果不是,请举出反例.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

相关试题

