【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
参考答案:
【答案】(1)y=﹣x+180;(2)y=(x﹣100)(﹣x+180)售价定为140元/件时,每天最大利润W=1600元.
【解析】(1)设y与x之间的函数关系式为y=kx+b(k≠0),根据所给函数图象列出关于kb的关系式,求出k、b的值即可;
(2)把每天的利润W与销售单价x之间的函数关系式化为二次函数顶点式的形式,由此关系式即可得出结论.
解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),由所给函数图象可知,
![]() ,解得
,解得![]() .
.
故y与x的函数关系式为y=﹣x+180;
(2)∵y=﹣x+180,
∴W=(x﹣100)y=(x﹣100)(﹣x+180)
=﹣x2+280x﹣18000
=﹣(x﹣140)2+1600,
∵a=﹣1<0,
∴当x=140时,W最大=1600,
∴售价定为140元/件时,每天最大利润W=1600元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=
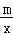 的图象的两个交点.
的图象的两个交点.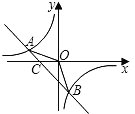
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求方程kx+b﹣
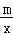 =0的解(请直接写出答案);
=0的解(请直接写出答案);(4)求不等式kx+b﹣
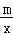 <0的解集(请直接写出答案).
<0的解集(请直接写出答案). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知 a+b=3,ab=2,则 a2+b2=________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
(2)如图2,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移
 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AB∥DC,AB=16cm,CD=10cm,AD=5cm DE⊥AB,垂足为E,点P从点A出发,以2cm/秒的速度沿AB向终点B运动;点Q从点C出发,以1cm/秒的速度沿CD向终点D运动(P,Q两点中,有一个点运动到终点时,所有运动即终止),设P,Q同时出发并运动了t秒.

(1)当四边形EPQD为矩形时,求t的值.
(2)当以点E、P、C、Q为顶点的四边形是平行四边形时,求t的值;
(3)探索:是否存在这样的t值,使三角形PDQ是以PD为腰的等腰三角形?若存在,求出t的值,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举行了一次“世博”知识竞赛.赛后抽取部分参赛同学的成绩进行整理,并制作成图表如下:

请根据以上图表提供的信息,解答下列问题:
(1)写出表格中m和n所表示的数:m= ,n= ,并补全频数分布直方图;
(2)抽取部分参赛同学的成绩的中位数落在第 组;
(3)如果比赛成绩80分以上(含80分)可以获得奖励,那么获奖率是多少?
相关试题

