Question

【题目】如图，已知A（﹣4，n），B（2，﹣4）是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点．

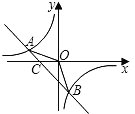
（1）求反比例函数和一次函数的解析式；

（2）求直线AB与x轴的交点C的坐标及△AOB的面积；

（3）求方程kx+b﹣=0的解（请直接写出答案）；

（4）求不等式kx+b﹣＜0的解集（请直接写出答案）．

Answer 1

【答案】（1）y=﹣．y=﹣x﹣2．（2）6（3）x1=﹣4，x2=2．（4）﹣4＜x＜0或x＞2．

【解析】

试题分析：根据待定系数法就可以求出函数的解析式；求函数的交点坐标就是求函数的解析式组成的方程组；求方程kx+b﹣=0的解即是求函数y=kx+b以函数y=的交点的横坐标．

解：（1）∵B（2，﹣4）在函数y=的图象上，

∴m=﹣8．

∴反比例函数的解析式为：y=﹣．

∵点A（﹣4，n）在函数y=﹣的图象上，

∴n=2，

∴A（﹣4，2），

∵y=kx+b经过A（﹣4，2），B（2，﹣4），

∴，解之得：．

∴一次函数的解析式为：y=﹣x﹣2．

（2）∵C是直线AB与x轴的交点，∴当y=0时，x=﹣2．

∴点C（﹣2，0），

∴OC=2．

∴S△AOB=S△ACO+S△BCO=OCn+OC×4=×2×2+×2×4=6．

（3）方程kx+b﹣=0的解，相当于一次函数y=kx+b的图象和反比例函数y=的图象的交点的横坐标，

即x1=﹣4，x2=2．

（4）不等式kx+b﹣＜0的解集相当于一次函数y=kx+b的函数值小于反比例函数y=的函数值，

从图象可以看出：﹣4＜x＜0或x＞2．