搜索
【题目】如图，在正方形纸片ABCD中，EF∥AD，M，N是线段EF的六等分点，若把该正方形纸片卷成一个圆柱，使点A与点D重合，此时，底面圆的直径为10cm，则圆柱上M，N两点间的距离是cm．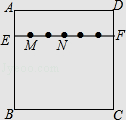 
参考答案：
【答案】5 
【解析】解：根据题意得：EF=AD=BC，MN=2EM= 
EF， 把该正方形纸片卷成一个圆柱，使点A与点D重合，则线段EF形成一直径为10cm的圆，线段EF为圆上的一段弧．
所对的圆心角为： ×360°=120°，
所以圆柱上M，N两点间的距离为：2×5×sin60°=5 cm．
故答案为：5 ．
根据题意得到MN= BC，当正方形纸片卷成一个圆柱时，EF卷成一个圆，线段卷成圆上一段弧，该段弧所对的圆心角为 ×360°，要求圆柱上M，N两点间的距离即求弦MN的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料：
小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如
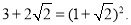善于思考的小明进行了以下探索：设
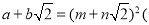其中a、b、m、n均为整数
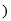，则有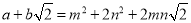
．
这样小明就找到了一种把类似
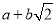的式子化为平方式的方法．请你仿照小明的方法探索并解决下列问题：
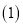当a、b、m、n均为正整数时，若
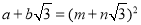，用含m、n的式子分别表示a、b，得： 
______， 
______；
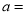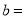利用所探索的结论，请找一组正整数a、b、m、n填空：______
_____
______
______
；
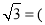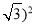若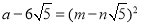
且a、m、n均为正整数，求a的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC中，∠A，∠B，∠C的对边分别为a、b、c，下列说法中错误的是（ ）
A．如果∠C－∠B＝∠A，则△ABC是直角三角形，且∠C＝90；
B．如果
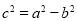，则△ABC是直角三角形，且∠C＝90；C．如果（c＋a）（ c－a）＝
，则△ABC是直角三角形，且∠C＝90；D．如果∠A：∠B：∠C＝3：2：5，则△ABC是直角三角形，且∠C＝90．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，关于 x，y 的方程组
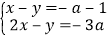的解满足 x＜0，y＞0．（1）x= ，y= （用含 a 的代数式表示）；
（2）求 a 的取值范围；
（3）若 2x8y=2m，用含有 a 的代数式表示 m，并求 m 的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点F在边AC上，并且CF=2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在4×5网格图中，其中每个小正方形边长均为1，梯形ABCD和五边形EFGHK的顶点均为小正方形的顶点．
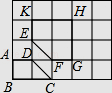
（1）以B为位似中心，在网格图中作四边形A′BC′D′，使四边形A′BC′D′和梯形ABCD位似，且位似比为2：1；
（2）求（1）中四边形A′BC′D′与五边形EFGHK重叠部分的周长．（结果保留根号） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，一幢楼房AB背后有一台阶CD，台阶每层高0.2米，且AC=17.2米，设太阳光线与水平地面的夹角为α，当α=60°时，测得楼房在地面上的影长AE=10米，现有一只小猫睡在台阶的MN这层上晒太阳．（
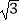取1.73）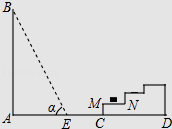 
（1）求楼房的高度约为多少米？
（2）过了一会儿，当α=45°时，问小猫能否还晒到太阳？请说明理由．
相关试题
