【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.( ![]() 取1.73)
取1.73) 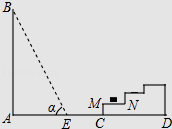
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.
参考答案:
【答案】
(1)解:当α=60°时,在Rt△ABE中,
∵tan60°= ![]() =
= ![]() ,
,
∴AB=10tan60°=10 ![]() ≈10×1.73=17.3米.
≈10×1.73=17.3米.
即楼房的高度约为17.3米;
(2)解:当α=45°时,小猫仍可以晒到太阳.理由如下:
假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.
∵∠BFA=45°,
∴tan45°= ![]() =1,
=1,
此时的影长AF=AB=17.3米,
∴CF=AF﹣AC=17.3﹣17.2=0.1米,
∴CH=CF=0.1米,
∴大楼的影子落在台阶MC这个侧面上,
∴小猫仍可以晒到太阳.
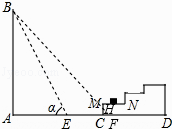
【解析】(1)在Rt△ABE中,由tan60°= ![]() =
= ![]() ,即可求出AB=10tan60°=17.3米;(2)假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.由∠BFA=45°,可得AF=AB=17.3米,那么CF=AF﹣AC=0.1米,CH=CF=0.1米,所以大楼的影子落在台阶MC这个侧面上,故小猫仍可以晒到太阳.
,即可求出AB=10tan60°=17.3米;(2)假设没有台阶,当α=45°时,从点B射下的光线与地面AD的交点为点F,与MC的交点为点H.由∠BFA=45°,可得AF=AB=17.3米,那么CF=AF﹣AC=0.1米,CH=CF=0.1米,所以大楼的影子落在台阶MC这个侧面上,故小猫仍可以晒到太阳.
-
科目: 来源: 题型:
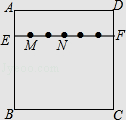
查看答案和解析>>【题目】如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在4×5网格图中,其中每个小正方形边长均为1,梯形ABCD和五边形EFGHK的顶点均为小正方形的顶点.
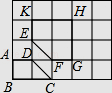
(1)以B为位似中心,在网格图中作四边形A′BC′D′,使四边形A′BC′D′和梯形ABCD位似,且位似比为2:1;
(2)求(1)中四边形A′BC′D′与五边形EFGHK重叠部分的周长.(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点G在对角线BD上
 不与点
不与点 重合
重合 于点
于点 于点F,连结AG.
于点F,连结AG. 写出线段
写出线段 长度之间的数量关系,并说明理由;
长度之间的数量关系,并说明理由; 若正方形ABCD的边长为
若正方形ABCD的边长为 ,求线段BG的长.
,求线段BG的长.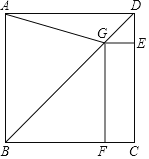
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,AD是
中,AD是 的中线,过点A作
的中线,过点A作 与AB的平行线DE交于点
与AB的平行线DE交于点 与AC相交于点O,连接EC.
与AC相交于点O,连接EC. 求证:
求证:  ;
; 当
当 满足条件______时,四边形ADCE是菱形,请补充条件并证明.
满足条件______时,四边形ADCE是菱形,请补充条件并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别
成绩x分
频数(人数)
第1组
50≤x<60
6
第2组
60≤x<70
8
第3组
70≤x<80
14
第4组
80≤x<90
a
第5组
90≤x<100
10
请结合图表完成下列各题:

(1)①表中a的值为; ②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是 .
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
相关试题

