【题目】如图,在4×5网格图中,其中每个小正方形边长均为1,梯形ABCD和五边形EFGHK的顶点均为小正方形的顶点.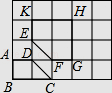
(1)以B为位似中心,在网格图中作四边形A′BC′D′,使四边形A′BC′D′和梯形ABCD位似,且位似比为2:1;
(2)求(1)中四边形A′BC′D′与五边形EFGHK重叠部分的周长.(结果保留根号)
参考答案:
【答案】
(1)
解:如图所示:四边形A′BC′D′就是所要求作的梯形;
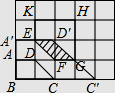
(2)
解:四边形A′BC′D′与五边形EFGHK重叠部分是平行四边形EFGD′,ED′=FG=1,
在Rt△EDF中,ED=DF=1,
由勾股定理得EF= ![]() =
= ![]() ,
,
∴D′G=EF= ![]() ,
,
∴四边形A′BC′D′与五边形EFGHK重叠部分的周长=ED′+FG+D′G+EF,
=1+1+ ![]() +
+ ![]() ,
,
=2+2 ![]() .
.
故答案为:2+2 ![]() .
.
【解析】(1)分别延长BA、BC、BD到A′、C′、D′,使BA′=2BA,BC′=2BC,BD′=2BD,然后顺次连接A′BC′D′即可得解;(2)根据网格图形,重叠部分正好是以格点为顶点的平行四边形,求出两邻边的长的,然后根据平行四边形的周长公式计算即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,关于 x,y 的方程组
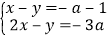 的解满足 x<0,y>0.
的解满足 x<0,y>0.(1)x= ,y= (用含 a 的代数式表示);
(2)求 a 的取值范围;
(3)若 2x8y=2m,用含有 a 的代数式表示 m,并求 m 的取值范围.
-
科目: 来源: 题型:
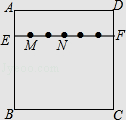
查看答案和解析>>【题目】如图,在正方形纸片ABCD中,EF∥AD,M,N是线段EF的六等分点,若把该正方形纸片卷成一个圆柱,使点A与点D重合,此时,底面圆的直径为10cm,则圆柱上M,N两点间的距离是cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的MN这层上晒太阳.(
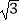 取1.73)
取1.73) 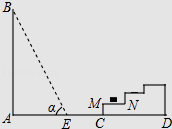
(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点G在对角线BD上
 不与点
不与点 重合
重合 于点
于点 于点F,连结AG.
于点F,连结AG. 写出线段
写出线段 长度之间的数量关系,并说明理由;
长度之间的数量关系,并说明理由; 若正方形ABCD的边长为
若正方形ABCD的边长为 ,求线段BG的长.
,求线段BG的长.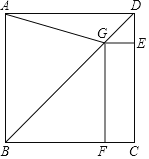
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,AD是
中,AD是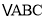 的中线,过点A作
的中线,过点A作 与AB的平行线DE交于点
与AB的平行线DE交于点 与AC相交于点O,连接EC.
与AC相交于点O,连接EC. 求证:
求证:  ;
; 当
当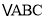 满足条件______时,四边形ADCE是菱形,请补充条件并证明.
满足条件______时,四边形ADCE是菱形,请补充条件并证明.
相关试题

