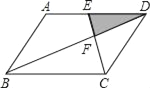
【题目】如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为( )
A. 8S B. 9S C. 10S D. 11S
参考答案:
【答案】B
【解析】分析:由于四边形ABCD是平行四边形,那么AD∥BC,AD=BC,根据平行线分线段成比例定理的推论可得△DEF∽△BCF,再根据E是AD中点,易求出相似比,从而可求![]() 的面积,再利用
的面积,再利用![]() 与
与![]() 是同高的三角形,则两个三角形面积比等于它们的底之比,从而易求
是同高的三角形,则两个三角形面积比等于它们的底之比,从而易求![]() 的面积,进而可求
的面积,进而可求![]() 的面积.
的面积.
详解:如图所示,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△DEF∽△BCF,
∴![]()
又∵E是AD中点,
∴![]()
∴DE:BC=DF:BF=1:2,
∴![]()
∴![]()
又∵DF:BF=1:2,
∴![]()
∴![]()
∴四边形ABCE的面积=9S,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家水果店以每千克2元的价格购进某种水果若干千克,然后以每千克4元的价格出售,每天可售出100千克,通过调查发现,这种水果每千克的售价每降低1元,每天可多售出200千克.
(1)若将这种水果每千克的售价降低
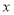 元,则每天销售量是多少千克?(结果用含
元,则每天销售量是多少千克?(结果用含 的代数式表示)
的代数式表示)(2)若想每天盈利300元,且保证每天至少售出260千克,那么水果店需将每千克的售价降低多少元?
-
科目: 来源: 题型:
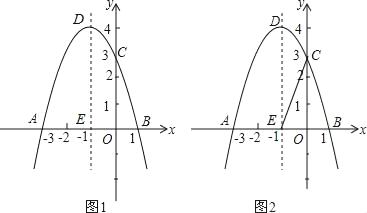
查看答案和解析>>【题目】如图1,关于x的二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.
(1)求抛物线的解析式;
(2)DE上是否存在点P到AD的距离与到x轴的距离相等?若存在求出点P,若不存在请说明理由;
(3)如图2,DE的左侧抛物线上是否存在点F,使2S△FBC=3S△EBC?若存在求出点F的坐标,若不存在请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)(单位:万人),其中9月30日的游客人数为2万:

(1)请问10月2日的游客人数为多少?
(2)请判断7天内游客人数最多的是哪天?最少的是哪天?它们相差多少万人?
(3)求这一次黄金周期间该风景区游客总人数.(假设每天游客都不重复)
-
科目: 来源: 题型:
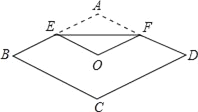
查看答案和解析>>【题目】如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF的长为( )
A. 2
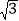 B. 2 C.
B. 2 C. 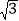 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有一组对边平行,有一个内角是它对角的一半的凸四边形叫做半对角四边形,如图1,直线
 ,点
,点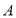 ,
, 在直线
在直线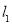 上,点
上,点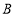 ,
,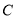 在直线
在直线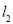 上,若
上,若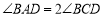 ,则四边形
,则四边形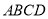 是半对角四边形.
是半对角四边形.(1)如图1,已知
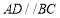 ,
, ,
,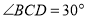 ,若直线
,若直线 ,
,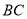 之间的距离为
之间的距离为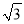 ,则AB的长是____,CD的长是______;
,则AB的长是____,CD的长是______;(2)如图2,点
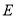 是矩形
是矩形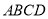 的边
的边 上一点,
上一点,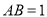 ,
,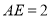 .若四边形
.若四边形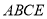 为半对角四边形,求
为半对角四边形,求 的长;
的长;(3)如图3,以
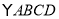 的顶点
的顶点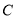 为坐标原点,边
为坐标原点,边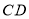 所在直线为
所在直线为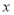 轴,对角线
轴,对角线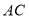 所在直线为
所在直线为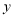 轴,建立平面直角坐标系.点
轴,建立平面直角坐标系.点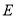 是边
是边 上一点,满足
上一点,满足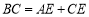 .
.①求证:四边形
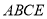 是半对角四边形;
是半对角四边形;②当
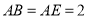 ,
,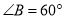 时,将四边形
时,将四边形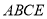 向右平移
向右平移 个单位后,恰有两个顶点落在反比例函数
个单位后,恰有两个顶点落在反比例函数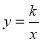 的图象上,求
的图象上,求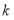 的值.
的值.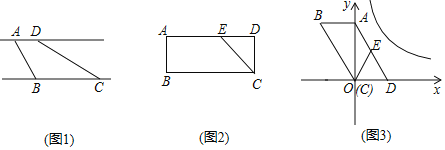
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
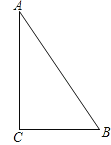
A.AB中点 B.BC中点 C. AC中点 D.∠C的平分线与AB的交点
相关试题

