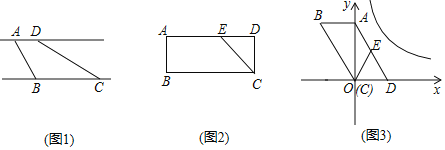
【题目】定义:有一组对边平行,有一个内角是它对角的一半的凸四边形叫做半对角四边形,如图1,直线![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 上,点
上,点![]() ,
,![]() 在直线
在直线![]() 上,若
上,若![]() ,则四边形
,则四边形![]() 是半对角四边形.
是半对角四边形.
(1)如图1,已知![]() ,
,![]() ,
,![]() ,若直线
,若直线![]() ,
,![]() 之间的距离为
之间的距离为![]() ,则AB的长是____,CD的长是______;
,则AB的长是____,CD的长是______;
(2)如图2,点![]() 是矩形
是矩形![]() 的边
的边![]() 上一点,
上一点,![]() ,
,![]() .若四边形
.若四边形![]() 为半对角四边形,求
为半对角四边形,求![]() 的长;
的长;
(3)如图3,以![]() 的顶点
的顶点![]() 为坐标原点,边
为坐标原点,边![]() 所在直线为
所在直线为![]() 轴,对角线
轴,对角线![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系.点
轴,建立平面直角坐标系.点![]() 是边
是边![]() 上一点,满足
上一点,满足![]() .
.
①求证:四边形![]() 是半对角四边形;
是半对角四边形;
②当![]() ,
,![]() 时,将四边形
时,将四边形![]() 向右平移
向右平移![]() 个单位后,恰有两个顶点落在反比例函数
个单位后,恰有两个顶点落在反比例函数![]() 的图象上,求
的图象上,求![]() 的值.
的值.
参考答案:
【答案】(1)2;![]() ;(2)AD=3;(3)①证明见解析;②
;(2)AD=3;(3)①证明见解析;②![]() 的值为为
的值为为![]() 或
或![]() .
.
【解析】
(1)过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,通过解直角三角形可求出
,通过解直角三角形可求出![]() ,
,![]() 的长;
的长;
(2)根据半对角四边形的定义可得出![]() ,进而可得出
,进而可得出![]() ,由等角对等边可得出
,由等角对等边可得出![]() ,结合
,结合![]() 即可求出
即可求出![]() 的长;
的长;
(3)①由平行四边形的性质可得出![]() ,
,![]() ,进而可得出
,进而可得出![]() ,根据等腰三角形的性质及三角形外角的性质可得出
,根据等腰三角形的性质及三角形外角的性质可得出![]() ,再结合半对角四边形的定义即可证出四边形
,再结合半对角四边形的定义即可证出四边形![]() 是半对角四边形;
是半对角四边形;
②由平行四边形的性质结合![]() ,
,![]() 可得出点
可得出点![]() ,
,![]() ,
,![]() 的坐标,分点
的坐标,分点![]() ,
,![]() 落在反比例函数图象上及点
落在反比例函数图象上及点![]() ,
,![]() 落在反比例函数图象上两种情况考虑:
落在反比例函数图象上两种情况考虑:![]() 利用平移的性质及反比例函数图象上点的坐标特征可得出关于
利用平移的性质及反比例函数图象上点的坐标特征可得出关于![]() 的一元一次方程,解之即可得出
的一元一次方程,解之即可得出![]() 值,再利用反比例函数图象上点的坐标特征可求出
值,再利用反比例函数图象上点的坐标特征可求出![]() 值;
值;![]() 同
同![]() 可求出
可求出![]() 值.综上,此题得解.
值.综上,此题得解.
解:(1)如图1,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.

![]() ,
,
![]() ,
,![]() .
.
在![]() 中,
中,![]() ;
;
在![]() 中,
中,![]() .
.
故答案为:2;![]() .
.
(2)如图2,

![]() 四边形
四边形![]() 为半对角四边形,
为半对角四边形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(3)如图3,

①证明![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]() 四边形
四边形![]() 是半对角四边形;
是半对角四边形;
②由题意,可知:点![]() 的坐标为
的坐标为![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
![]() 当点
当点![]() ,
,![]() 向右平移
向右平移![]() 个单位后落在反比例函数的图象上时,
个单位后落在反比例函数的图象上时,![]() ,
,
解得:![]() ,
,
![]() ;
;
![]() 当点
当点![]() ,
,![]() 向右平移
向右平移![]() 个单位后落在反比例函数的图象上时,
个单位后落在反比例函数的图象上时,
![]() ,
,
解得:![]() ,
,
![]() .
.
综上所述:![]() 的值为为
的值为为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)(单位:万人),其中9月30日的游客人数为2万:

(1)请问10月2日的游客人数为多少?
(2)请判断7天内游客人数最多的是哪天?最少的是哪天?它们相差多少万人?
(3)求这一次黄金周期间该风景区游客总人数.(假设每天游客都不重复)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为( )
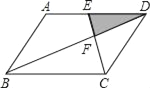
A. 8S B. 9S C. 10S D. 11S
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF的长为( )
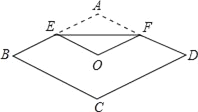
A. 2
 B. 2 C.
B. 2 C. 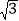 D. 4
D. 4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
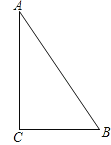
A.AB中点 B.BC中点 C. AC中点 D.∠C的平分线与AB的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的半径是4,点A,B,C在⊙O上,若四边形OABC为菱形,则图中阴影部分面积为( )
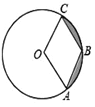
A.
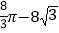 B.
B. 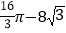 C.
C. 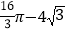 D.
D. 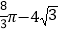
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕顶点C旋转得到△A′B′C,且点B刚好落在A′B′上.若∠A=25°,∠BCA′=45°,则∠A′BA等于( )
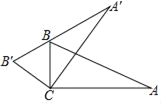
A. 40°B. 35°C. 30°D. 45°
相关试题

