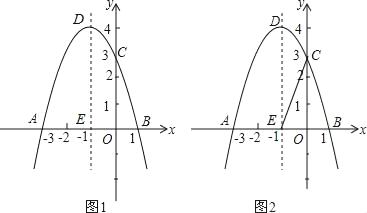
【题目】如图1,关于x的二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.
(1)求抛物线的解析式;
(2)DE上是否存在点P到AD的距离与到x轴的距离相等?若存在求出点P,若不存在请说明理由;
(3)如图2,DE的左侧抛物线上是否存在点F,使2S△FBC=3S△EBC?若存在求出点F的坐标,若不存在请说明理由.
参考答案:
【答案】(1)y=﹣x2﹣2x+3(2)(﹣1,![]() ﹣1)或(﹣1,﹣
﹣1)或(﹣1,﹣![]() ﹣1);(3)F(
﹣1);(3)F(![]() ,
,![]() )
)
【解析】分析:(1)把A、C两点坐标代入可求得b、c,可求得抛物线解析式;
(2)当点P在∠DAB的平分线上时,过P作PM⊥AD,设出P点坐标,可表示出PM、PE,由角平分线的性质可得到PM=PE,可求得P点坐标;当点P在∠DAB外角平分线上时,同理可求得P点坐标;
(3)可先求得△FBC的面积,过F作FQ⊥x轴,交BC的延长线于Q,可求得FQ的长,可设出F点坐标,表示出B点坐标,从而可表示出FQ的长,可求得F点坐标.
详解:(1)∵二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),
∴![]() ,解得
,解得![]() ,
,
∴抛物线的解析式y=﹣x2﹣2x+3,
(2)存在,
当P在∠DAB的平分线上时,如图1,作PM⊥AD,
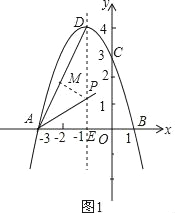
设P(﹣1,m),则PM=PDsin∠ADE=![]() (4﹣m),PE=m,
(4﹣m),PE=m,
∵PM=PE,
∴![]() (4﹣m)=m,m=
(4﹣m)=m,m=![]() ﹣1,
﹣1,
∴P点坐标为(﹣1,![]() ﹣1);
﹣1);
当P在∠DAB的外角平分线上时,如图2,作PN⊥AD,
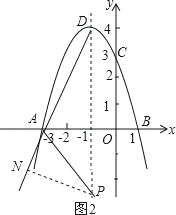
设P(﹣1,n),则PN=PDsin∠ADE=![]() (4﹣n),PE=﹣n,
(4﹣n),PE=﹣n,
∵PN=PE,
∴![]() (4﹣n)=﹣n,n=﹣
(4﹣n)=﹣n,n=﹣![]() ﹣1,
﹣1,
∴P点坐标为(﹣1,﹣![]() ﹣1);
﹣1);
综上可知存在满足条件的P点,其坐标为(﹣1,![]() ﹣1)或(﹣1,﹣
﹣1)或(﹣1,﹣![]() ﹣1);
﹣1);
(3)∵抛物线的解析式y=﹣x2﹣2x+3,
∴B(1,0),
∴S△EBC=![]() EBOC=3,
EBOC=3,
∵2S△FBC=3S△EBC,
∴S△FBC=![]() ,
,
过F作FQ⊥x轴于点H,交BC的延长线于Q,过F作FM⊥y轴于点M,如图3,

∵S△FBC=S△BQH﹣S△BFH﹣S△CFQ=![]() HBHQ﹣
HBHQ﹣![]() BHHF﹣
BHHF﹣![]() QFFM=
QFFM=![]() BH(HQ﹣HF)﹣
BH(HQ﹣HF)﹣![]() QFFM=
QFFM=![]() BHQF﹣
BHQF﹣![]() QFFM=
QFFM=![]() QF(BH﹣FM)=
QF(BH﹣FM)=![]() FQOB=
FQOB=![]() FQ=
FQ=![]() ,
,
∴FQ=9,
∵BC的解析式为y=﹣3x+3,
设F(x0,﹣x02﹣2x0+3),
∴﹣3x0+3+x02+2x0﹣3=9,
解得:x0=![]() 或
或![]() (舍去),
(舍去),
∴点F的坐标是(![]() ,
,![]() ),
),
∵S△ABC=6>![]() ,
,
∴点F不可能在A点下方,
综上可知F点的坐标为(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级一班某次数学测验的优秀成绩为80分,数学老师以优秀成绩为基准,记作0,把小龙、小聪、小梅、小莉、小刚这五位同学的成绩简记为+10,–15,0,+20,–2.问这五位同学的实际成绩分别是多少分?优秀率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.
性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等.
理解:如图①,在△ABC中,CD是AB边上的中线,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S△BCD.
应用:如图②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF与BE交于点O.
(1)求证:△AOB和△AOE是“友好三角形”;
(2)连接OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积.
探究:在△ABC中,∠A=30°,AB=4,点D在线段AB上,连接CD,△ACD和△BCD是“友好三角形”,将△ACD沿CD所在直线翻折,得到△A′CD,若△A′CD与△ABC重合部分的面积等于△ABC面积的
 ,请直接写出△ABC的面积.
,请直接写出△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一家水果店以每千克2元的价格购进某种水果若干千克,然后以每千克4元的价格出售,每天可售出100千克,通过调查发现,这种水果每千克的售价每降低1元,每天可多售出200千克.
(1)若将这种水果每千克的售价降低
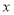 元,则每天销售量是多少千克?(结果用含
元,则每天销售量是多少千克?(结果用含 的代数式表示)
的代数式表示)(2)若想每天盈利300元,且保证每天至少售出260千克,那么水果店需将每千克的售价降低多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“十一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)(单位:万人),其中9月30日的游客人数为2万:

(1)请问10月2日的游客人数为多少?
(2)请判断7天内游客人数最多的是哪天?最少的是哪天?它们相差多少万人?
(3)求这一次黄金周期间该风景区游客总人数.(假设每天游客都不重复)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为( )
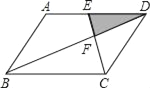
A. 8S B. 9S C. 10S D. 11S
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF的长为( )
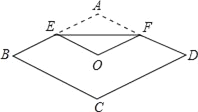
A. 2
 B. 2 C.
B. 2 C. 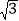 D. 4
D. 4
相关试题

