【题目】如图,平面直角坐标系xOy中,双曲线y=![]() (x>0)与直线y=kx-k的交点为点A(m,2).
(x>0)与直线y=kx-k的交点为点A(m,2).
(1) 求k的值;
(2) 当x>0时,直接写出不等式kx-k ≤![]() 的解集:_ ;
的解集:_ ;
(3) 设直线y=kx-k与y轴交于点B,若C是x轴上一点,且满足△ABC的面积是4,求点C的坐标.

参考答案:
【答案】(1)k=2 ;(2)0<x≤2;(3)C(-1,0)或(3,0)
【解析】分析: (1)利用待定系数法即可解决问题.
(2)观察图象,直线y=kx-k的图象在y=![]() 的下方(包括交点A),由此可以写出不等式的解集.
的下方(包括交点A),由此可以写出不等式的解集.
(3)设点C坐标(m,0),直线y=2x-2与x轴的交点D坐标为(1,0),根据S△ABC=S△CDA+S△CDB=4,列出方程即可解决.
详解: (1)∵点A在双曲线y=![]() 上,
上,
∴2=![]() ,
,
∴m=2,
∴点A(2,2).
∵点A在直线y=kx-k上,
∴2=2k-k,
∴k=2.
(2)由图象可知,x>0时,不等式kx-k≤![]() 的解集为0<x≤2.
的解集为0<x≤2.
故答案为0<x≤2.
(3)设点C坐标(m,0).
∵直线y=2x-2与x轴的交点D坐标为(1,0),与y轴的交点B坐标为为(0,-2),
∴S△ABC=S△CDA+S△CDB=4,
∴![]() |m-1|×(2+2)=4,
|m-1|×(2+2)=4,
∴m=3或-1.
∴点C坐标为(3,0)或(-1,0).

-
科目: 来源: 题型:
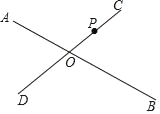
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,P是CD上一点,
(1)过点P作AB的垂线段PE;
(2)过点P作CD的垂线,与AB相交于点F;
(3)将线段PE、PF、FO从小到大排列为_____,这样排列的依据是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知将一副三角板(直角三角板OAB和直角三角板OCD,∠AOB=90°,∠ABO=45°,∠CDO=90°,∠COD=60°)
(1)如图1摆放,点O、A、C在一直线上,则∠BOD的度数是多少?
(2)如图2,将直角三角板OCD绕点O逆时针方向转动,若要OB恰好平分∠COD,则∠AOC的度数是多少?
(3)如图3,当三角板OCD摆放在∠AOB内部时,作射线OM平分∠AOC,射线ON平分∠BOD,如果三角板OCD在∠AOB内绕点O任意转动,∠MON的度数是否发生变化?如果不变,求其值;如果变化,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程mx2+(3﹣m)x﹣3=0(m为实数,m≠0).
(1) 试说明:此方程总有两个实数根.
(2) 如果此方程的两个实数根都为正整数,求整数m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,点E是平面内异于点A的任意一点,以线
段AE为边作正方形AEFG,连接EB,GD.
(1) 如图1,判断EB与GD的关系并说明理由;
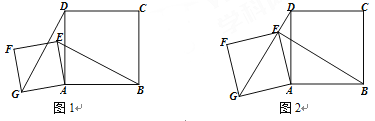
(2) 如图2,若点E在线段DG上,AB=5,AG=3
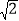 ,求BE的长.
,求BE的长. -
科目: 来源: 题型:
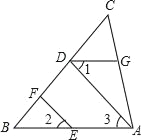
查看答案和解析>>【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= ( )
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵ ,(已知)
∴∠AGD= (等式性质)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=
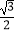 ,则∠CDE+∠ACD=( )
,则∠CDE+∠ACD=( ) 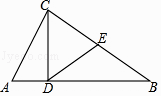
A.60°
B.75°
C.90°
D.105°
相关试题

