【题目】如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE= ![]() ,则∠CDE+∠ACD=( )
,则∠CDE+∠ACD=( ) 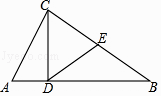
A.60°
B.75°
C.90°
D.105°
参考答案:
【答案】C
【解析】解:∵CD⊥AB,E为BC边的中点, ∴BC=2CE= ![]() ,
,
∵AB=2,AC=1,
∴AC2+BC2=12+( ![]() )2=4=22=AB2 ,
)2=4=22=AB2 ,
∴∠ACB=90°,
∵tan∠A= ![]() =
= ![]() ,
,
∴∠A=60°,
∴∠ACD=∠B=30°,
∴∠DCE=60°,
∵DE=CE,
∴∠CDE=60°,
∴∠CDE+∠ACD=90°,
故选C.
【考点精析】通过灵活运用直角三角形斜边上的中线和勾股定理的逆定理,掌握直角三角形斜边上的中线等于斜边的一半;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若c<0,则(1﹣a)c+|c|等于( )
A.﹣ac
B.ac
C.2c﹣ac
D.2c+ac -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )
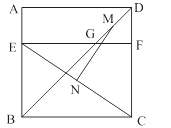
A.3
B.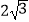
C.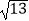
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】点A(﹣3,2)关于x轴的对称点A′的坐标为 .
-
科目: 来源: 题型:
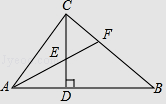
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
A.
B.
C.
D.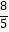
-
科目: 来源: 题型:
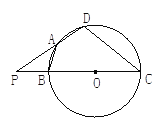
查看答案和解析>>【题目】如图,四边形ABCD内接于以BC为直径的圆O,且AB=AD,延长CB、DA交于P,当PB=BO,CD=18时,求:
(1)⊙O的半径长;
(2)PA的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2+a﹣3=0,那么a2(a+4)的值是( )
A.﹣18
B.﹣15
C.﹣12
D.9
相关试题

