【题目】已知数轴上有![]() 两点,分别表示的数为
两点,分别表示的数为![]() 和
和![]() ,且
,且![]() ,点
,点![]() 以每秒3个单位长度的速度沿数轴向左匀速运动,点
以每秒3个单位长度的速度沿数轴向左匀速运动,点![]() 以每秒2个单位长度的速度向右匀速运动.设运动时间为
以每秒2个单位长度的速度向右匀速运动.设运动时间为![]() 秒(
秒(![]() ).
).
(1)![]() ______,
______,![]() ______;
______;
(2)运动开始前,![]() 两点之间的距离为________;
两点之间的距离为________;
(3)它们按上述方式运动,![]() 两点经过多少秒会相遇?相遇点所表示的数是什么?
两点经过多少秒会相遇?相遇点所表示的数是什么?
(4)当![]() 为多少秒时,
为多少秒时,![]() 两点之间的距离为2?请直接写出结果.
两点之间的距离为2?请直接写出结果.
参考答案:
【答案】(1)12;38(2)50(3)10秒,相遇点所表示的数是18.(4)t为![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)利用绝对值的非负性,可求出a,b值;
(2)由点A,B表示的数可求出线段AB的长;
(3)当运动时间为t秒时,点A表示的数为3t+12,点B表示的数为2t38,由A,B两点相遇,可得出关于t的一元一次方程,解之即可得出结论;
(4)根据线段AB=2,即可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论.
(1)∵|a12|+|b+38|=0,
∴a12=0,b+38=0,
∴a=12,b=38.
故答案为:12;38.
(2)AB=12(38)=50.
故答案为:50.
(3)当运动时间为t秒时,点A表示的数为3t+12,点B表示的数为2t38,
依题意,得:3t+12=2t38,
解得:t=10.
∴3t+12=18.
答:A,B两点经过10秒会相遇,相遇点所表示的数是18.
(4)依题意,得:|3t+12(2t38)|=2,
即505t=2或5t50=2,
解得:t=![]() 或t=
或t=![]() .
.
答:当t为![]() 秒或
秒或![]() 秒时,A,B两点之间的距离为2.
秒时,A,B两点之间的距离为2.
-
科目: 来源: 题型:
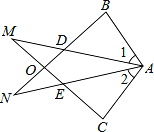
查看答案和解析>>【题目】已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)求证:BD=CE;
(2)求证:∠M=∠N.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2+2x﹣3与x轴交于A,B两点(点A在点B的左侧),将这条抛物线向右平移m(m>0)个单位长度,平移后的抛物线与x轴交于C,D两点(点C在点D的左侧),若B,C是线段AD的三等分点,则m的值为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将连续的奇数1,3,5,7,9,…排成如图所示的数表,用一个“
 ”形框框住任意七个数.
”形框框住任意七个数.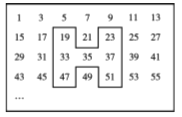
(1)若“
 ”形框中间的奇数为
”形框中间的奇数为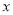 ,那么框中的七个数之和用含
,那么框中的七个数之和用含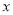 的代数式可表示为_______;
的代数式可表示为_______;(2)若落在“
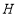 ”形框中间且又是第二列的奇数17,31,45,…,则这一列数可以用代数式表示为
”形框中间且又是第二列的奇数17,31,45,…,则这一列数可以用代数式表示为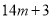 (
(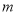 为正整数),同样,落在“
为正整数),同样,落在“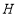 ”形框中间又是第三列的奇数可表示为______(用含
”形框中间又是第三列的奇数可表示为______(用含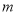 的代数式表示);
的代数式表示);(3)被“
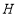 ”形框框住的七个数之和能否等于1057?如果能,请求出中间的奇数,并直接说明这个奇数落在从左往右的第几列;如果不能,请写出理由.
”形框框住的七个数之和能否等于1057?如果能,请求出中间的奇数,并直接说明这个奇数落在从左往右的第几列;如果不能,请写出理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
(1)若固定三根木条AB,BC,AD不动,AB=AD=2cm,BC=5cm,如图,量得第四根木条CD=5cm,判断此时∠B与∠D是否相等,并说明理由.
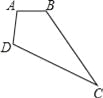
(2)若固定一根木条AB不动,AB=2cm,量得木条CD=5cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A、C、D能构成周长为30cm的三角形,求出木条AD,BC的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市开展的“阳光体育”跳绳活动中,为了了解中学生跳绳活动的开展情况,随机抽查了全市七年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制两个不完整的统计图.请根据图中提供的信息,解答下列问题:
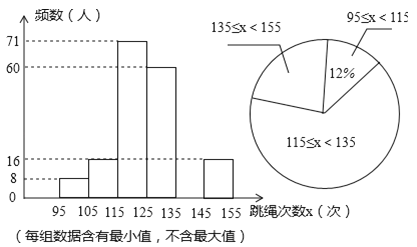
(1)本次共抽查了多少名学生?
(2)请补全频数分布直方图空缺部分,其中扇形统计图中表示跳绳次数范围135≤x<155的扇形的圆心角度数为 度.
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市28000名七年级学生中有多少名学生的成绩为优秀?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
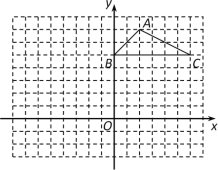
(1) 点A的坐标为 ,点C的坐标为 ;
(2) 将△ABC先向左平移3个单位长度,再向下平移6个单位长度,请画出平移后的△A1B1C1;
(3) 连接A1B,A1 C,△A1BC的面积= .
相关试题

