【题目】为提升青少年的身体素质,郑州市在全市中小学推行“阳光体育”活动,河南省实验中学为满足学生的需求,准备再购买一些篮球和足球.如果分别用800元购买篮球和足球,购买篮球的个数比足球的个数少2个,足球的单价为篮球单价的![]() .
.
(1)求篮球、足球的单价分别为多少元?
(2)学校计划用不多于5200元购买篮球、足球共60个,那么至少购买多少个足球?
(3)在(2)的条件下,若篮球数量不能低过15个,那么有多少种购买方案?哪种方案费用最少?最少费用是多少?
参考答案:
【答案】(1)篮球的单价为100元/个,足球的单价为80元/个;(2)至少要购买40个足球;(3)6种方案,买足球45个,篮球15个费用最少,最少费用是5100元.
【解析】
(1)设篮球的单价为x元/个,则足球的单价为0.8x元/个,根据用800元购买篮球的个数比购买足球的个数少2个,即可得出关于x的分式方程,解方程即得结果;
(2)设购买m个足球,则购买(60﹣m)个篮球,根据总价=单价×购买数量结合总价钱不多于5200元,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,取其范围内的最小正整数即可;
(3)由篮球数量不能低过15个并结合(2)题的结果可得关于m的取值范围,进而可得相应的购买方案;设总费用为w元,由题意可得w与m的一次函数关系式,然后根据一次函数的性质即可得到结论.
解:(1)设篮球的单价为x元/个,则足球的单价为0.8x元/个,
根据题意得:![]() ,解得:x=100,
,解得:x=100,
经检验,x=100是原方程的解,∴0.8x=80.
答:篮球的单价为100元/个,足球的单价为80元/个;
(2)设购买m个足球,则购买(60﹣m)个篮球,
根据题意得:80m+100(60﹣m)≤5200,解得:m≥40.
答:至少要购买40个足球;
(3)由题意得,60﹣m≥15,解得:m≤45,
∵m≥40,∴40≤m≤45,
∵m为整数,∴m可取40,41,42,43,44,45,共6种购买方案;
设总费用为w元,由题意得,w=80m+100(60﹣m)=﹣20m+6000,
∵﹣20<0,∴w随着m的增大而减小,
∴当m=45时,w最小=5100,
答:共有6种购买方案,买足球45个,篮球15个费用最少,最少费用是5100元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=90°,OC为一条射线,OE,OF分别平分∠AOC,∠BOC,那么∠EOF 的度数为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“奇特数”.例如:
 ,
, ,
, ;则8、16、24这三个数都是奇特数.
;则8、16、24这三个数都是奇特数.
(1)填空:32___________奇特数,2018_________奇特数.(填“是”或者“不是”)
(2)设两个连续奇数是
 和
和 (其中
(其中 取正整数),由这两个连续奇数构造的奇特数是8的倍数吗?为什么?
取正整数),由这两个连续奇数构造的奇特数是8的倍数吗?为什么?(3)如图所示,拼叠的正方形边长是从1开始的连续奇数…,按此规律拼叠到正方形
 ,其边长为403,求阴影部分的面积.
,其边长为403,求阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 于
于 点,
点, ,点
,点 是
是 边上一点,连接
边上一点,连接 并延长,交
并延长,交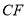 于
于 点,
点, .
.
(1)
 与
与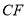 有什么位置关系,说明理由;
有什么位置关系,说明理由;(2)若
 ,
, ,求
,求 的度数和
的度数和 的长度;
的长度;(3)在(2)的条件下,若将
 绕着点
绕着点 顺时针旋转
顺时针旋转 ,则(1)中结论是否仍然成立?如果成立,请证明;如果不成立,请直接写出此时
,则(1)中结论是否仍然成立?如果成立,请证明;如果不成立,请直接写出此时 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列内容,并答题:我们知道,计算n边形的对角线条数公式为:
 n(n﹣3).
n(n﹣3).如果一个n边形共有20条对角线,那么可以得到方程
 n(n﹣3)=20 .
n(n﹣3)=20 .整理得n2﹣3n﹣40=0;解得n=8或n=﹣5
∵n为大于等于3的整数,∴n=﹣5不合题意,舍去.
∴n=8,即多边形是八边形.
根据以上内容,问:
(1)若一个多边形共有14条对角线,求这个多边形的边数;
(2)A同学说:“我求得一个多边形共有10条对角线”,你认为A同学说法正确吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1)(1,1),(1,2),(2,2)……根据这个规律,第2019个点的坐标为________

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠BDC,∠2+∠3=180°.
(1) 请你判断DA与CE的位置关系,并说明理由;
(2) 若DA平分∠BDC,CE⊥AE于点E,∠1=70°,试求∠FAB的度数.

相关试题

