【题目】如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“奇特数”.例如:![]() ,
,![]() ,
,![]() ;则8、16、24这三个数都是奇特数.
;则8、16、24这三个数都是奇特数.

(1)填空:32___________奇特数,2018_________奇特数.(填“是”或者“不是”)
(2)设两个连续奇数是![]() 和
和![]() (其中
(其中![]() 取正整数),由这两个连续奇数构造的奇特数是8的倍数吗?为什么?
取正整数),由这两个连续奇数构造的奇特数是8的倍数吗?为什么?
(3)如图所示,拼叠的正方形边长是从1开始的连续奇数…,按此规律拼叠到正方形![]() ,其边长为403,求阴影部分的面积.
,其边长为403,求阴影部分的面积.
参考答案:
【答案】(1)是;不是;(2)是,理由详见解析;(2)81608
【解析】
(1)根据奇特数的概念进行判断即可;
(2)利用平方差公式计算![]() ,即可得到;两个连续奇数构造的奇特数是
,即可得到;两个连续奇数构造的奇特数是![]() 的倍数;
的倍数;
(3)利用阴影部分面积为![]() ,进而求得答案即可.
,进而求得答案即可.
解:(1)∵![]()
∴![]() 是奇特数;
是奇特数;
∵8、16、24这三个数都是奇特数,它们都是![]() 的倍数,而
的倍数,而![]() 不是
不是![]() 的倍数
的倍数
∴![]() 不是奇特数;
不是奇特数;
(2)结论:两个连续奇数构造的奇特数是![]() 的倍数
的倍数
理由:∵![]()
![]()
![]()
![]()
∴两个连续奇数构造的奇特数是![]() 的倍数;
的倍数;
(3)![]()
![]()
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为
 BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )
A. 点E B. 点F C. 点M D. 点N
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点
 是第一象限内的点,直线
是第一象限内的点,直线 与
与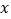 轴交于点
轴交于点 ,过点
,过点 作
作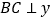 轴,垂足为
轴,垂足为 ,过点
,过点 的直线与
的直线与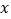 轴交于点
轴交于点 ,已知直线
,已知直线 上的点的坐标
上的点的坐标 是方程的
是方程的 解,直线
解,直线 上的点的坐标
上的点的坐标 是方程
是方程 的解
的解(1)求点
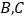 的坐标
的坐标(2)证明:
 (要求写出每一步的推理依据);
(要求写出每一步的推理依据);(3)求点
 的坐标,并求三角形
的坐标,并求三角形 的面积
的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=90°,OC为一条射线,OE,OF分别平分∠AOC,∠BOC,那么∠EOF 的度数为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 于
于 点,
点, ,点
,点 是
是 边上一点,连接
边上一点,连接 并延长,交
并延长,交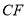 于
于 点,
点, .
.
(1)
 与
与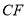 有什么位置关系,说明理由;
有什么位置关系,说明理由;(2)若
 ,
, ,求
,求 的度数和
的度数和 的长度;
的长度;(3)在(2)的条件下,若将
 绕着点
绕着点 顺时针旋转
顺时针旋转 ,则(1)中结论是否仍然成立?如果成立,请证明;如果不成立,请直接写出此时
,则(1)中结论是否仍然成立?如果成立,请证明;如果不成立,请直接写出此时 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】为提升青少年的身体素质,郑州市在全市中小学推行“阳光体育”活动,河南省实验中学为满足学生的需求,准备再购买一些篮球和足球.如果分别用800元购买篮球和足球,购买篮球的个数比足球的个数少2个,足球的单价为篮球单价的
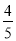 .
.(1)求篮球、足球的单价分别为多少元?
(2)学校计划用不多于5200元购买篮球、足球共60个,那么至少购买多少个足球?
(3)在(2)的条件下,若篮球数量不能低过15个,那么有多少种购买方案?哪种方案费用最少?最少费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列内容,并答题:我们知道,计算n边形的对角线条数公式为:
 n(n﹣3).
n(n﹣3).如果一个n边形共有20条对角线,那么可以得到方程
 n(n﹣3)=20 .
n(n﹣3)=20 .整理得n2﹣3n﹣40=0;解得n=8或n=﹣5
∵n为大于等于3的整数,∴n=﹣5不合题意,舍去.
∴n=8,即多边形是八边形.
根据以上内容,问:
(1)若一个多边形共有14条对角线,求这个多边形的边数;
(2)A同学说:“我求得一个多边形共有10条对角线”,你认为A同学说法正确吗?为什么?
相关试题

