【题目】问题:探究函数y=|x|-1的性质.
小凡同学根据学习函数的经验,对函数y=|x|-1的图象与性质进行了探究.下面是小凡的探究过程,请补充完整:
(1)在函数y=|x|-1中,自变量x的取值范围是______________;
(2)下表是y与x的几组对应值.
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | ||
y | 2 | 1 | 0 | -1 | 0 | 1 | m |
①m=_________;
②若A(n,9),B(10,9)为该函数图象上不同的两点,则_n=__________;
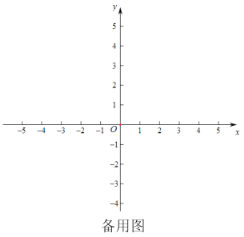
(3)如下图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;

(4)结合函数图象,解决问题:
①函数的最小值为________;
②已知直线![]() 与函数
与函数![]() 的图象交于C,D两点,当y1≥y时x的取值范围是___________.
的图象交于C,D两点,当y1≥y时x的取值范围是___________.
参考答案:
【答案】(1)全体实数(或任意实数) (2)①2 ②-10 (3)作图见解析 (4)①-1 ②![]()
【解析】
(1)根据函数和图象的性质,写出自变量x的取值范围即可;
(2)①根据函数解析式求出m的值即可;②根据函数解析式求出n的值即可;
(3)利用描点法作出图象即可;
(4)①根据图象求出最小值即可;②分情况讨论:1)当![]() 时,2)当
时,2)当![]() 时,分别列不等式求解即可.
时,分别列不等式求解即可.
(1)根据函数和图象的性质可得,自变量x的取值范围是全体实数(或任意实数);
(2)①令![]() ,则
,则![]() ;
;
②∵A(n,9),B(10,9)为该函数图象上不同的两点
∴![]() 且
且![]()
解得![]() ;
;
(3)如图所示,即为所求;

(4)①如图所示,当![]() 时,函数有最小值,最小值为-1;
时,函数有最小值,最小值为-1;
②1)当![]() 时,
时,
∵![]()
∴![]()
解得![]()
∴![]()
2)当![]() 时,
时,
∵![]()
∴![]()
解得![]()
∴![]()
综上所述,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在方格纸中
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A′B′C′;
(3)计算△A′B′C′的面积S.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,一次函数y=kx+5(x>-5)的图象G经过点A(-2,3),直线
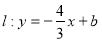 与图象G交于点B,与x轴交于点C.
与图象G交于点B,与x轴交于点C.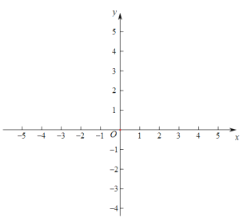
(1)求k的值;
(2)横、纵坐标都是整数的点叫做整点.记图象G在点A,B之间的部分与线段OA,OC,BC围成的区域(不含边界)为W.
①当b=2时,直接写出区域W内的整点个数;
②区域W内恰有3个整点,结合函数图象,求b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,正方形ABCD,点P是直线BC上一个动点,连接PD交直线AB于点O,过点B作BE⊥PD于点E,连接AE.



(1)如图1,
①直接写出∠AED的度数;
②用等式表示线段AE、BE和DE之间的数量关系,并证明;
(2)当点P运动到图2和图3所示的位置时,请选择其中一种情况补全图形,并接写出线段AE、BE和DE之间的数量关系.
-
科目: 来源: 题型:
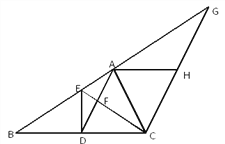
查看答案和解析>>【题目】在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.过C点作CG∥AD,交BA的延长线于G,过A作BC的平行线交CG于H点.
(1)若∠BAC=900,求证:四边形ADCH是菱形;
(2)求证:△ABC∽△FCD;
(3)若DE=3,BC=8,求△FCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a、b满足a=
 +
+ ﹣1,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
﹣1,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC.
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)
 的值是否发生变化,并说明理由.
的值是否发生变化,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=kx-2与坐标轴所围图形的面积为3,点A(3,m)是直线y=kx-2上一点.
(1)求点A的坐标;
(2)点P在y轴上,且∠PAO=30°,直接写出点P坐标.
相关试题

