搜索
【题目】在平面直角坐标系xOy中，一次函数y=kx+5（x>-5）的图象G经过点A（-2，3），直线
与图象G交于点B，与x轴交于点C．
（1）求k的值；
（2）横、纵坐标都是整数的点叫做整点．记图象G在点A，B之间的部分与线段OA，OC，BC围成的区域（不含边界）为W．
①当b=2时，直接写出区域W内的整点个数；
②区域W内恰有3个整点，结合函数图象，求b的取值范围．
参考答案：
【答案】（1）
（2）①3 ②
或
【解析】
（1）将点
代入
中，即可求出k的值；
（2）①根据题意作图，再根据图形求出整点的个数；②分两种情况：1）当直线l在OA上方时，2）当直线l在OA下方时，画图计算边界时点b的值，即可求出b的取值范围．
（1）将点代入中
解得；
（2）①当
时，图象如图所示
可得
∴区域W内的整点有
，共3个；
②1）当直线l在OA上方时
∵区域W内恰有3个整点，
∴区域W内的整点有
当直线l过点
时，
；当直线l过点
时，
∴
2）当直线l在OA下方时
∵区域W内恰有3个整点，
∴区域W内的整点有
当直线l过点
时，
；当直线l过点
时，
∴
综上所述，或．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．
（1）求证：△ABE≌△CDF；
（2）若AB=DB，猜想：四边形DFBE是什么特殊的四边形？并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】用硬纸板剪一个平行四边形ABCD，作出它的对角线的交点O，我们可以做如下操作：
用大头针把一根平放在平行四边形上的直细木条固定在点O处，并使细木条可以绕点O转动，拨动细木条，它可以停留在任意位置. 如果设细木条与一组对边AB，CD的交点分别为点E，F，则下列结论：①OE=OF；②AE=CF；③BE=DF；④△AOE≌△COF，其中一定成立的是_________________________（填写序号即可）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC在方格纸中
（1）请在方格纸上建立平面直角坐标系，使A（2，3），C（6，2），并求出B点坐标；
（2）以原点O为位似中心，相似比为2，在第一象限内将△ABC放大，画出放大后的图形△A′B′C′；
（3）计算△A′B′C′的面积S．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，正方形ABCD，点P是直线BC上一个动点，连接PD交直线AB于点O，过点B作BE⊥PD于点E，连接AE．
（1）如图1，
①直接写出∠AED的度数；
②用等式表示线段AE、BE和DE之间的数量关系，并证明；
（2）当点P运动到图2和图3所示的位置时，请选择其中一种情况补全图形，并接写出线段AE、BE和DE之间的数量关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题：探究函数y=|x|-1的性质．
小凡同学根据学习函数的经验，对函数y=|x|-1的图象与性质进行了探究．下面是小凡的探究过程，请补充完整：
（1）在函数y=|x|-1中，自变量x的取值范围是______________；
（2）下表是y与x的几组对应值．
x
-3
-2
-1
0
1
2
3
y
2
1
0
-1
0
1
m
①m=_________；
②若A（n，9），B（10，9）为该函数图象上不同的两点，则_n=__________；
（3）如下图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；
（4）结合函数图象，解决问题：
①函数的最小值为________；
②已知直线
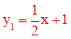与函数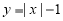
的图象交于C，D两点，当y1≥y时x的取值范围是___________． -
科目： 来源： 题型：
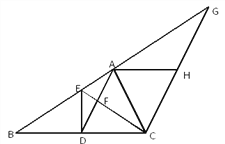
查看答案和解析>>【题目】在△ABC中，D是BC的中点，且AD＝AC，DE⊥BC，与AB相交于点E，EC与AD相交于点F．过C点作CG∥AD，交BA的延长线于G，过A作BC的平行线交CG于H点．
（1）若∠BAC＝900，求证：四边形ADCH是菱形；
（2）求证：△ABC∽△FCD；
（3）若DE＝3，BC＝8，求△FCD的面积．
相关试题
