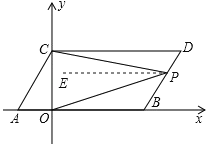
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a、b满足a=![]() +
+![]() ﹣1,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
﹣1,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC.
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)![]() 的值是否发生变化,并说明理由.
的值是否发生变化,并说明理由.
参考答案:
【答案】(1)8;(2)点P的坐标为(0,4)或(0,﹣4);(3)比值不变.
【解析】
试题分析:(1)根据被开方数大于等于0列式求出b,再求出a,从而得到A、B的坐标,再根据向上平移纵坐标加,向右平移横坐标加求出点C、D的坐标即可,然后利用平行四边形的面积公式列式计算即可得解;
(2)根据三角形的面积公式列出方程求出OP,再分点P在y轴正半轴和负半轴两种情况讨论求解;
(3)根据平移的性质可得AB∥CD,再过点P作PE∥AB,根据平行公理可得PE∥CD,然后根据两直线平行,内错角相等可得∠DCP=∠CPE,∠BOP=∠OPE,然后求出∠CPO=∠DCP+∠BOP,从而判断出比值不变.
解:(1)由题意得,3﹣b≥0且b﹣3≥0,
解得b≤3且b≥3,
∴b=3,
a=﹣1,
∴A(﹣1,0),B(3,0),
∵点A,B分别向上平移2个单位,再向右平移1个单位,
∴点C(0,2),D(4,2);
∵AB=3﹣(﹣1)=3+1=4,
∴S四边形ABDC=4×2=8;
(2)∵S△PAB=S四边形ABDC,
∴![]() ×4OP=8,
×4OP=8,
解得OP=4,
∴点P的坐标为(0,4)或(0,﹣4);
(3)![]() =1,比值不变.
=1,比值不变.
理由如下:由平移的性质可得AB∥CD,
如图,过点P作PE∥AB,则PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP,
∴![]() =1,比值不变.
=1,比值不变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正常人的心跳平均每分70次,一天大约跳100800次,将100800用科学记数法表示为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算 (4*6=24分)
(1) x·(-x2)·x3;
(2)
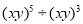
(3)a5.(-a)3+(-2a2)4;
(4)
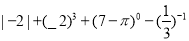
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°,则下列结论:
①∠BOE=
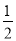 (180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.
(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的个数有多少个?( )
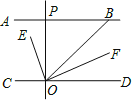
A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,已知∠A=4∠B=104°,则∠C的度数是( )
A. 50° B. 45° C. 40° D. 30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A的坐标为(1,3),点B的坐标为(2,1).将线段AB沿某一方向平移后,点A的对应点的坐标为(﹣2,1).则点B的对应点的坐标为( )
A. (5,3) B. (﹣1,﹣2) C. (﹣1,﹣1) D. (0,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%.设把x公顷旱地改为林地,则可列方程( )
A.54﹣x=20%×108
B.54﹣x=20%(108+x)
C.54+x=20%×162
D.108﹣x=20%(54+x)
相关试题

