【题目】直线y=kx-2与坐标轴所围图形的面积为3,点A(3,m)是直线y=kx-2上一点.
(1)求点A的坐标;
(2)点P在y轴上,且∠PAO=30°,直接写出点P坐标.
参考答案:
【答案】(1)点A的坐标为![]() 或
或![]() (2)点P的坐标为
(2)点P的坐标为![]() 或
或![]() 或
或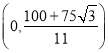 或
或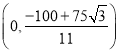
【解析】
(1)先求出k的值,再代入求出m的值即可;
(2)分情况讨论:①当点A的坐标为![]() 时,如图1,②当点A的坐标是
时,如图1,②当点A的坐标是![]() 时,如图2,③当点A的坐标是
时,如图2,③当点A的坐标是![]() 时,如图3,根据相似三角形的性质以及判定定理、勾股定理、解直角三角形进行求解即可.
时,如图3,根据相似三角形的性质以及判定定理、勾股定理、解直角三角形进行求解即可.
(1)当![]() ,则
,则![]() ,当
,当![]() ,则
,则![]()
∴直线y=kx-2与坐标轴的交点坐标为![]() 和
和![]()
∵直线y=kx-2与坐标轴所围图形的面积为3
∴![]()
解得![]()
当![]() 时,
时,![]() ,可得
,可得![]()
当![]() 时,
时,![]() ,可得
,可得![]()
故点A的坐标为![]() 或
或![]() ;
;
(2)①当点A的坐标为![]() 时,如图1
时,如图1
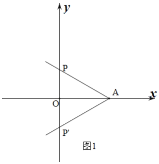
设![]()
∵在![]() 中,
中,![]()
![]()
![]()
![]()
![]()
![]()
∴点![]() 或点
或点![]()
②当点A的坐标是![]() 时,如图2时
时,如图2时
作PB⊥AO于B,AC⊥y轴于点C,则![]() ,
,![]()

设![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
整理得
![]()
解得![]() (负值不合题意舍去)
(负值不合题意舍去)
![]()
∴P的坐标为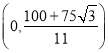
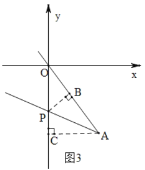
③当点A的坐标是![]() 时,如图3时
时,如图3时
作PB⊥AO于点B,AC⊥y轴于点C,则![]() ,
,![]()
设![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
整理得
![]()
解得![]() (负值不合题意舍去)
(负值不合题意舍去)
![]()
∴P的坐标为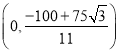
综上所述,点P的坐标为![]() 或
或![]() 或
或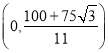 或
或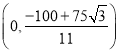 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:探究函数y=|x|-1的性质.
小凡同学根据学习函数的经验,对函数y=|x|-1的图象与性质进行了探究.下面是小凡的探究过程,请补充完整:
(1)在函数y=|x|-1中,自变量x的取值范围是______________;
(2)下表是y与x的几组对应值.
x
-3
-2
-1
0
1
2
3
y
2
1
0
-1
0
1
m
①m=_________;
②若A(n,9),B(10,9)为该函数图象上不同的两点,则_n=__________;
(3)如下图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;

(4)结合函数图象,解决问题:
①函数的最小值为________;
②已知直线
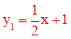 与函数
与函数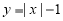 的图象交于C,D两点,当y1≥y时x的取值范围是___________.
的图象交于C,D两点,当y1≥y时x的取值范围是___________. -
科目: 来源: 题型:
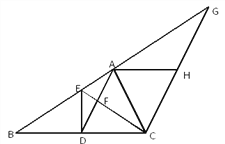
查看答案和解析>>【题目】在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.过C点作CG∥AD,交BA的延长线于G,过A作BC的平行线交CG于H点.
(1)若∠BAC=900,求证:四边形ADCH是菱形;
(2)求证:△ABC∽△FCD;
(3)若DE=3,BC=8,求△FCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a、b满足a=
 +
+ ﹣1,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
﹣1,现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC.
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)
 的值是否发生变化,并说明理由.
的值是否发生变化,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
-
科目: 来源: 题型:
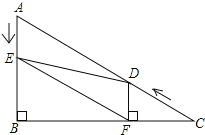
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,BC=
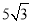 ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在平面直角坐标系中,作出下列各点,A(-3,4), B(-3,-2),O(0,0),并把各点连起来.
(2)画出△ABO先向下平移2个单位,再向右平移4 个单位得到的图形△A1B1o1,并直接写出A1坐标
(3) 直接写出三角形ABO的面积.
相关试题

