搜索
【题目】观察下列关于
、
的单项式的特点：
，
，
，
，
……按此规律，第10个单项式是（ ）
A.
B.
C.
D.
参考答案：
【答案】D
【解析】
首先判断符号规律为奇数个为正，偶数个为负，再依次找到系数的分子变化规律，系数的分母变化规律，及a的次数变化规律.
观察式子可知符号规律为奇数个为正，偶数个为负，
∴第10个单项式的符号为负，
∵系数的分子变化为2,6,12,20,30…依次+4，+6，+8，+10
故第10个单项式系数的分子为2+4+6+8+10+12+14+16+18+20=110，
系数的分母变化为3,5,8,13,21…依次+2，+3，+5，+8，为加上前两次所加的和，
则分母依次为3，2+3，3+5,5+8,8+13,13+21,21+34,34+55,55+89,89+144
故第10个单项式系数的分母为89+144=233，
a的次数为每次增加1
故第10个单项式是
故选D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下表是小明某一周的收支情况，规定收入为正，支出为负.（单位：元）
周一
周二
周三
周四
周五
周六
周日
15
12
0
20
15
10
14
8
12
19
10
9
11
8
（1）小明哪天的收入小于支出？答：
（2）小明这一周的平均支出是多少？
（3）小明这一周共有多少节余？
-
科目： 来源： 题型：
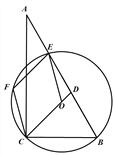
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，∠A=30°，经过B，C两点的⊙O交边AB于另一点E，延长CO交边AB于点D，EF∥CD交⊙O于另一点F， 连接CF。
（1）若⊙O的半径为4，求弧CE的长；
（2）求证：四边形EFCO是菱形;
（3）若BC=6，tan∠CDB=3，求BD的长。
-
科目： 来源： 题型：
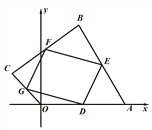
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，四边形OABC的顶点A在x轴的正半轴上，OA=4，OC=2，点D、E、F、G分别为边OA、AB、BC、CO的中点，连结DE、EF、FG、GD.
（1）若点C在y轴的正半轴上，当点B的坐标为（2，4）时，判断四边形DEFG的形状，并说明理由.
（2）若点C在第二象限运动，且四边形DEFG为菱形时，求点四边形OABC对角线OB长度的取值范围.
（3）若在点C的运动过程中，四边形DEFG始终为正方形，当点C从X轴负半轴经过Y轴正半轴，运动至X轴正半轴时，直接写出点B的运动路径长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，AB=AC，E，D，F分别是边AB，BC，AC的中点．
（1）求证：四边形AEDF是菱形；
（2）若∠B=30°，BC=4
，求四边形AEDF的周长． -
科目： 来源： 题型：
查看答案和解析>>【题目】有一条长度为 a 的线段.
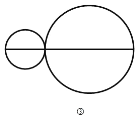
（1）如图①，以该线段为直径画一个圆，该圆的周长 C1 = ；如图②，分别以该线段的一半为直 径画两个圆，这两个圆的周长的和 C2 = （都用含 a 的代数式表示，结果保留 ）
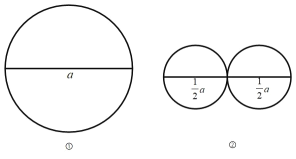
（2）如图③，在该线段上任取一点，再分别以两条小线段为直径画两个圆，这两个圆的周长的和为 C3 ,探索 C1 和 C3 的数量关系，并说明理由。
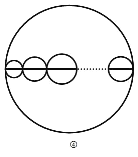
（3）如图④，当 a =10 时，以该线段为直径画一个大圆，再在大圆内画若干个小圆，这些小圆的直径都和 大圆的直径在同一条直线上，且小圆的直径的和等于大圆的直径，那么图中所有圆的周长的和为 （结 果保留 ）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，A（0，1），B（0，
），C（3，0）．
（1）若以A、B、C、D为顶点的四边形是平行四边形，则请你写出所有符合条件的D点坐标.
（2）直接写出一个符合（1）中条件的直线AD 的解析式.
（3）求平行四边形ABCD的面积.
相关试题
