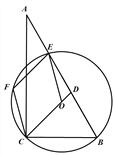
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,经过B,C两点的⊙O交边AB于另一点E,延长CO交边AB于点D,EF∥CD交⊙O于另一点F, 连接CF。
(1)若⊙O的半径为4,求弧CE的长;
(2)求证:四边形EFCO是菱形;
(3)若BC=6,tan∠CDB=3,求BD的长。
参考答案:
【答案】(1)![]() (2)证明见解析(3)3+
(2)证明见解析(3)3+![]()
【解析】分析:(1)根据圆周角定理可得∠COE=120°,再根据弧长计算公式即可得解;
(2)如图,连接OF,易证△OEF和△OCF是等边三角形,得EF=OE=CF=OC,故得四边形EFCO是菱形;
(3)作CH⊥AB于点H,可得∠CHD=∠CHE=90°,在Rt△CHB中,∠ABC=60°,BC=6,故BH=3,CH=![]() .在Rt△CHD中,tan∠CDB=3,故DH=
.在Rt△CHD中,tan∠CDB=3,故DH=![]() CH=
CH=![]() ,故BD=3+
,故BD=3+![]() .
.
(1)∵∠ACB=90°,∠A=30°,
∴∠ABC=60°
∴∠COE=120°
∴弧CE的长![]()
(2)如图,连接OF,
∵∠COE=120°,
∴∠DOE=60°,
∵EF∥CD,
∴∠OEF=60°,
∵OE=OF,
∴△OEF是等边三角形,
∴EF= OE =r,∠FOE=60°,
∴∠COE=∠COE-60°=60°,
∵OC=OF,
∴△OCF是等边三角形,
∴CF=OC=r,
∴EF=OE=CF=OC,
∴四边形EFCO是菱形.
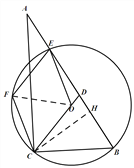
(3)作CH⊥AB于点H,可得∠CHD=∠CHE=90°,
在Rt△CHB中,
∵∠ABC=60°,BC=6,
∴BH=3,CH=![]() .
.
在Rt△CHD中,tan∠CDB=3,
∴DH=![]() CH=
CH=![]() ,
,
∴BD=3+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在二次函数y=ax2+bx+c的图象中,你认为其中正确的是( )
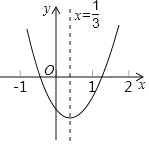
A. a>0 B. c>0
C. b2﹣4ac<0 D. 一元二次方程ax2+bx+c=0有两个相等实根
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
幻方的历史很悠久,传说中最早出现在夏禹时代的“洛书”,用今天的数学符号翻译出来,就是一个三阶幻方,即将若干个数组成一个正方形数阵,任意一行、一列及对角线上的数字之和都相等.如图1,就是一个三阶幻方,由1,2,3,4,5,6,7,8,9九个数字组成的一个三行三列的矩阵(如图),其对角线、横行、纵向的和都为15.
(1)探究:研究发现三阶幻方中间的数字与9个数的和有确定的数量关系.如果设数字连续性三阶幻方中间的数字是a,则幻方中9个数字之和是 (用含a的字母代数式表示)
(2)应用:请你选取一组数据构造一个三阶幻方,填入到如图2的3×3方格中,使得每行、每列、每条对角线上的三个数之和都等于21;


(3)拓展:
数阵是由幻方演化出来的另一种数字图.将连续的奇数1,3,5,7,9…排列成数阵(如图3),用十字框随机框出5个数,十字框中的五数之和能等于2020吗?并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是小明某一周的收支情况,规定收入为正,支出为负.(单位:元)
周一
周二
周三
周四
周五
周六
周日
15
12
0
20
15
10
14
8
12
19
10
9
11
8
(1)小明哪天的收入小于支出?答:
(2)小明这一周的平均支出是多少?
(3)小明这一周共有多少节余?
-
科目: 来源: 题型:
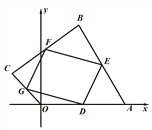
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,四边形OABC的顶点A在x轴的正半轴上,OA=4,OC=2,点D、E、F、G分别为边OA、AB、BC、CO的中点,连结DE、EF、FG、GD.
(1)若点C在y轴的正半轴上,当点B的坐标为(2,4)时,判断四边形DEFG的形状,并说明理由.
(2)若点C在第二象限运动,且四边形DEFG为菱形时,求点四边形OABC对角线OB长度的取值范围.
(3)若在点C的运动过程中,四边形DEFG始终为正方形,当点C从X轴负半轴经过Y轴正半轴,运动至X轴正半轴时,直接写出点B的运动路径长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列关于
 、
、 的单项式的特点:
的单项式的特点: ,
, ,
, ,
, ,
, ……按此规律,第10个单项式是( )
……按此规律,第10个单项式是( )A.
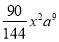 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,E,D,F分别是边AB,BC,AC的中点.

(1)求证:四边形AEDF是菱形;
(2)若∠B=30°,BC=4
 ,求四边形AEDF的周长.
,求四边形AEDF的周长.
相关试题

