【题目】有一条长度为 a 的线段.
(1)如图①,以该线段为直径画一个圆,该圆的周长 C1 = ;如图②,分别以该线段的一半为直 径画两个圆,这两个圆的周长的和 C2 = (都用含 a 的代数式表示,结果保留 )
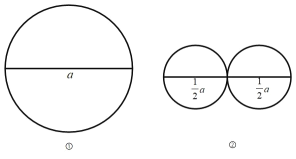
(2)如图③,在该线段上任取一点,再分别以两条小线段为直径画两个圆,这两个圆的周长的和为 C3 ,探索 C1 和 C3 的数量关系,并说明理由。
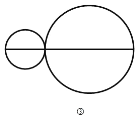
(3)如图④,当 a =10 时,以该线段为直径画一个大圆,再在大圆内画若干个小圆,这些小圆的直径都和 大圆的直径在同一条直线上,且小圆的直径的和等于大圆的直径,那么图中所有圆的周长的和为 (结 果保留 )
参考答案:
【答案】(1)![]() ;
;![]() ;(2) C1= C3,理由见解析;(3)
;(2) C1= C3,理由见解析;(3)![]()
【解析】
(1)运用圆的周长公式计算即可;
(2)可设其中一圆直径为x,则另一圆直径为![]() ,再利用圆的周长公式计算即可比较;
,再利用圆的周长公式计算即可比较;
(3)可设图中小圆直径分别为![]() ,其中
,其中 ![]() ,再利用圆的周长公式计算即可.
,再利用圆的周长公式计算即可.
解:(1)由圆的周长公式得:圆的周长=![]() ;故
;故![]() ,
,![]() ;
;
(2)设其中一个圆的直径为x,则其周长为:![]() ;
;
则另一圆的直径为![]() ,其周长为:
,其周长为:![]() ;
;
所以![]() ,
,
故![]() ;
;
(3)设图中小圆直径分别为![]() ,其中
,其中 ![]() ,
,
图中所有小圆的周长为:![]()
![]() ;
;
图中所有圆的周长=所有小圆的周长+大圆周长=![]()
-
科目: 来源: 题型:
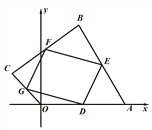
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,四边形OABC的顶点A在x轴的正半轴上,OA=4,OC=2,点D、E、F、G分别为边OA、AB、BC、CO的中点,连结DE、EF、FG、GD.
(1)若点C在y轴的正半轴上,当点B的坐标为(2,4)时,判断四边形DEFG的形状,并说明理由.
(2)若点C在第二象限运动,且四边形DEFG为菱形时,求点四边形OABC对角线OB长度的取值范围.
(3)若在点C的运动过程中,四边形DEFG始终为正方形,当点C从X轴负半轴经过Y轴正半轴,运动至X轴正半轴时,直接写出点B的运动路径长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列关于
 、
、 的单项式的特点:
的单项式的特点: ,
, ,
, ,
, ,
, ……按此规律,第10个单项式是( )
……按此规律,第10个单项式是( )A.
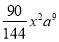 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,E,D,F分别是边AB,BC,AC的中点.

(1)求证:四边形AEDF是菱形;
(2)若∠B=30°,BC=4
 ,求四边形AEDF的周长.
,求四边形AEDF的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(0,1),B(0,
 ),C(3,0).
),C(3,0).
(1)若以A、B、C、D为顶点的四边形是平行四边形,则请你写出所有符合条件的D点坐标.
(2)直接写出一个符合(1)中条件的直线AD 的解析式.
(3)求平行四边形ABCD的面积.
-
科目: 来源: 题型:
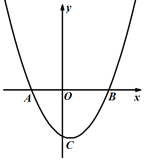
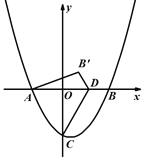
查看答案和解析>>【题目】如图,抛物线
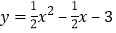 分别交x轴于点A,B(点A在点B的左侧),交y轴于点C,D为线段AB上一点,连接CD,作点B关于CD的对称点B′,连接AB′,B′D .
分别交x轴于点A,B(点A在点B的左侧),交y轴于点C,D为线段AB上一点,连接CD,作点B关于CD的对称点B′,连接AB′,B′D .(1)求点A,B的坐标.
(2)当点B′落坐标轴上时,求点D的坐标.
(3)在点D的运动过程中,△AB′D 的内角能否等于45°,若能,求此时点B′的坐标;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分类是研究问题的一种常用方法,我们在学习有理数和代数式的相关概念、运算法则时,除了 学到了具体知识,还学会了分类思考,在进行分类时,我们首先应明确分类标准,其次要做到分类时既不 重复,也不遗漏。
(初步感受)(1)在对多项式
 ,
, 进行分类时,如果以项数作为分类标准,可以分为哪几类?如果以次数作为分类标准,可以分为哪几类?
进行分类时,如果以项数作为分类标准,可以分为哪几类?如果以次数作为分类标准,可以分为哪几类?(简单运用)(2)已知 a, b 是有理数,比较 a b 与 a b的大小;
(深入思考)(3)已知 a, b c 是有理数,且 ca b>ca b ,判断 b, c 的符号,并说明理由。
相关试题

