【题目】下表是小明某一周的收支情况,规定收入为正,支出为负.(单位:元)
周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
15 | 12 | 0 | 20 | 15 | 10 | 14 |
8 | 12 | 19 | 10 | 9 | 11 | 8 |
(1)小明哪天的收入小于支出?答:
(2)小明这一周的平均支出是多少?
(3)小明这一周共有多少节余?
参考答案:
【答案】(1)周三、周六;(2)11元;(3)9元
【解析】
(1)每天对应的数据相加,结果为负数的即为收入小于支出;
(2)将所有的用负号表示的数的绝对值加起来除以一周的天数即可;
(3)将所有用正号表示的数相加的和减去所有用负号表示的数的绝对值的和所得到的差即为所求.
解:
(1)由题意得:要比较小明的收入小于支出,将每天对应数据相加,结果为负数则收入小于支出;得只有周三:![]() ;周六:
;周六:![]() ,故周三,周六的收入小于支出;
,故周三,周六的收入小于支出;
(2) 8 12 19 10 9 11 8 7 11元
(3) 15 12 20 15 10 14 77 9 元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平行四边形ABCD在平面直角坐标系中,A、B(点A在点B的左侧)两点的横坐标是方程
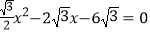 的两个根,点D在y轴上其中
的两个根,点D在y轴上其中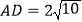 .
.
(1)求平行四边形ABCD的面积;
(2)若P是第一象限位于直线BD上方的一点,过P作
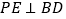 于E,过E作
于E,过E作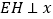 轴于H点,作PF∥y轴交直线BD于F,F为BD中点,其中△PEF的周长是
轴于H点,作PF∥y轴交直线BD于F,F为BD中点,其中△PEF的周长是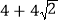 ;若M为线段AD上一动点,N为直线BD上一动点,连接HN,NM,求
;若M为线段AD上一动点,N为直线BD上一动点,连接HN,NM,求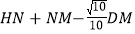 的最小值,此时y轴上有一个动点G,当
的最小值,此时y轴上有一个动点G,当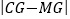 最大时,求G点坐标;
最大时,求G点坐标;(3)在(2)的情况下,将△AOD绕O点逆时针旋转60°后得到
 如图2,将线段
如图2,将线段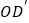 沿着x轴平移,记平移过程中的线段
沿着x轴平移,记平移过程中的线段 为
为 ,在平面直角坐标系中是否存在点S,使得以点
,在平面直角坐标系中是否存在点S,使得以点 ,
, ,E,S为顶点的四边形为菱形,若存在,请求出点S的坐标,若不存在,请说明理由.
,E,S为顶点的四边形为菱形,若存在,请求出点S的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在二次函数y=ax2+bx+c的图象中,你认为其中正确的是( )
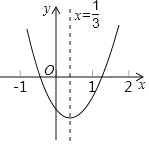
A. a>0 B. c>0
C. b2﹣4ac<0 D. 一元二次方程ax2+bx+c=0有两个相等实根
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
幻方的历史很悠久,传说中最早出现在夏禹时代的“洛书”,用今天的数学符号翻译出来,就是一个三阶幻方,即将若干个数组成一个正方形数阵,任意一行、一列及对角线上的数字之和都相等.如图1,就是一个三阶幻方,由1,2,3,4,5,6,7,8,9九个数字组成的一个三行三列的矩阵(如图),其对角线、横行、纵向的和都为15.
(1)探究:研究发现三阶幻方中间的数字与9个数的和有确定的数量关系.如果设数字连续性三阶幻方中间的数字是a,则幻方中9个数字之和是 (用含a的字母代数式表示)
(2)应用:请你选取一组数据构造一个三阶幻方,填入到如图2的3×3方格中,使得每行、每列、每条对角线上的三个数之和都等于21;


(3)拓展:
数阵是由幻方演化出来的另一种数字图.将连续的奇数1,3,5,7,9…排列成数阵(如图3),用十字框随机框出5个数,十字框中的五数之和能等于2020吗?并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,经过B,C两点的⊙O交边AB于另一点E,延长CO交边AB于点D,EF∥CD交⊙O于另一点F, 连接CF。
(1)若⊙O的半径为4,求弧CE的长;
(2)求证:四边形EFCO是菱形;
(3)若BC=6,tan∠CDB=3,求BD的长。
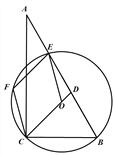
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,四边形OABC的顶点A在x轴的正半轴上,OA=4,OC=2,点D、E、F、G分别为边OA、AB、BC、CO的中点,连结DE、EF、FG、GD.
(1)若点C在y轴的正半轴上,当点B的坐标为(2,4)时,判断四边形DEFG的形状,并说明理由.
(2)若点C在第二象限运动,且四边形DEFG为菱形时,求点四边形OABC对角线OB长度的取值范围.
(3)若在点C的运动过程中,四边形DEFG始终为正方形,当点C从X轴负半轴经过Y轴正半轴,运动至X轴正半轴时,直接写出点B的运动路径长.
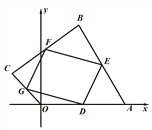
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列关于
 、
、 的单项式的特点:
的单项式的特点: ,
, ,
, ,
, ,
, ……按此规律,第10个单项式是( )
……按此规律,第10个单项式是( )A.
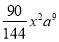 B.
B. C.
C. D.
D.
相关试题

