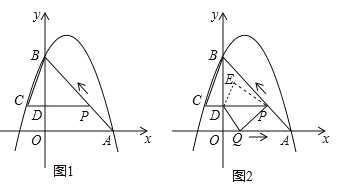
【题目】如图 1,二次函数![]() 的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接 BC ,当t=![]() 时,求△BCP的面积;
时,求△BCP的面积;
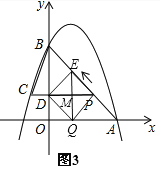
(3)如图 2,动点 P 从 A 出发时,动点 Q 同时从 O 出发,在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动,当点 P 与 B 重合时,P 、 Q 两点同时停止运动,连接 DQ 、 PQ ,将△DPQ沿直线 PC 折叠到 △DPE .在运动过程中,设 △DPE 和 △OAB重合部分的面积为 S ,直接写出 S 与 t 的函数关系式及 t 的取值范围.
参考答案:
【答案】(1)![]() ;(2)4;(3)
;(2)4;(3)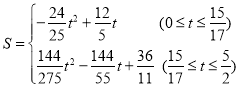 .
.
【解析】
试题分析:(1)直接将A、B两点的坐标代入列方程组解出即可;
(2)如图1,要想求△BCP的面积,必须求对应的底和高,即PC和BD;先求OD,再求BD,PC是利用点P和点C的横坐标求出,要注意符号;
(3)分两种情况讨论:①△DPE完全在△OAB中时,即当![]() 时,如图2所示,重合部分的面积为S就是△DPE的面积;②△DPE有一部分在△OAB中时,当
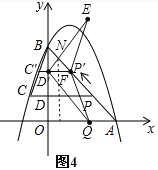
时,如图2所示,重合部分的面积为S就是△DPE的面积;②△DPE有一部分在△OAB中时,当![]() 时,如图4所示,△PDN就是重合部分的面积S.
时,如图4所示,△PDN就是重合部分的面积S.
试题解析:(1)把A(3,0),B(0,4)代入![]() 中得:
中得:
![]() ,解得:
,解得:![]() ,∴解析式为:
,∴解析式为:![]() ;
;
(2)如图1,当![]() 时,AP=2t,∵PC∥x轴,∴
时,AP=2t,∵PC∥x轴,∴![]() ,∴
,∴![]() ,∴OD=
,∴OD=![]() =
=![]() =
=![]() ,当y=
,当y=![]() 时,
时,![]() =
=![]() ,
,![]() ,解得:
,解得:![]() ,
,![]() ,∴C(﹣1,
,∴C(﹣1,![]() ),由
),由![]() ,得
,得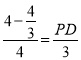 ,则PD=2,∴S△BCP=
,则PD=2,∴S△BCP=![]() ×PC×BD=
×PC×BD=![]() =4;
=4;
(3)分两种情况讨论:①如图3,当点E在AB上时,由(2)得OD=QM=ME=![]() ,∴EQ=
,∴EQ=![]() ,由折叠得:EQ⊥PD,则EQ∥y轴,∴
,由折叠得:EQ⊥PD,则EQ∥y轴,∴![]() ,∴
,∴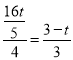 ,∴t=
,∴t=![]() ,同理得:PD=
,同理得:PD=![]() ,∴当
,∴当![]() 时,S=S△PDQ=
时,S=S△PDQ=![]() ×PD×MQ=
×PD×MQ=![]() ,
,![]() ;
;
②当![]() 时,如图4,P′D′=
时,如图4,P′D′=![]() ,点Q与点E关于直线P′C′对称,则Q(t,0)、E(t,
,点Q与点E关于直线P′C′对称,则Q(t,0)、E(t,![]() ),∵AB的解析式为:
),∵AB的解析式为:![]() ,D′E的解析式为:
,D′E的解析式为:![]() ,则交点N(
,则交点N(![]() ,
,![]() ),∴S=S△P′D′N=
),∴S=S△P′D′N=![]() ×P′D′×FN=
×P′D′×FN=![]() ,∴
,∴![]() .
.
综上所述: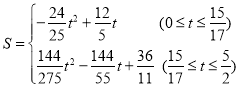 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OA=OB,OC=OD,AD和BC相交于点E,则图中共有全等三角形的对数( )

A. 2对 B. 3对 C. 4对 D. 5对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD⊥AB于点D,点E在CD上,下列四个条件:①AD=ED;②∠A=∠BED;③∠C=∠B;④AC=EB,将其中两个作为条件,不能判定△ADC≌△EDB的是
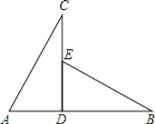
A.①②B.①④C.②③D.②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,下列结论:①△ABD≌△CDB;②∠BFE=∠BDC;③S△ABE=S△DEF;④AB=6,AD=8,DB=10,则AE=4.其中正确的个数为( )
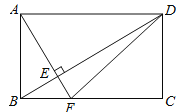
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用
 ,
, 表示直角三角形的两直角边(
表示直角三角形的两直角边( ),下列四个说法:
),下列四个说法:
①
 ,②
,② ,③
,③ ,④
,④ .
.其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ADC=90°,AD=8m,CD=6m,BC=24m,AB=26m,则图中阴影部分的面积为_________;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24cm,CF=3cm,则制成整个金属框架所需这种材料的总长度为 ________cm.

相关试题

