【题目】如图,在长方形ABCD中,AF⊥BD于E,AF交BC于点F,连接DF,下列结论:①△ABD≌△CDB;②∠BFE=∠BDC;③S△ABE=S△DEF;④AB=6,AD=8,DB=10,则AE=4.其中正确的个数为( )
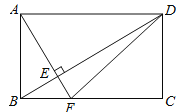
A.1个B.2个C.3个D.4个
参考答案:
【答案】C
【解析】
在长方形ABCD中有AB=CD,AD=CB,BD=DB,根据SSS可证△ABD≌△CDB,①正确;根据同角的余角相等可证∠BFE=∠BDC,②正确;由同底等高的三角形面积相等可得S△ABD= S△ADF,两边同时减去S△ADE可得S△ABE=S△DEF,③正确;根据△ABD面积的不同求法可求出AE=4.8,④错误,问题得解.
解:在长方形ABCD中,
∵AB=CD,AD=CB,BD=DB,
∴△ABD≌△CDB(SSS),故①正确;
∵AF⊥BD,
∴在Rt△BEF中,∠BFE+∠FBE=90°,
∵在Rt△ACD中,∠CBD+∠BDC=90°,
∴∠BFE=∠BDC,故②正确;
∵S△ABD=![]() ,S△ADF=
,S△ADF=![]() ,
,
∴S△ABD= S△ADF,
∴S△ABD-S△ADE = S△ADF-S△ADE,即S△ABE=S△DEF,故③正确;
∵AB=6,AD=8,DB=10,
∴S△ABD=![]() ,
,
∴![]() ,故④错误,
,故④错误,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,公路MN和公路PG在点P处交汇,点A处有一所中学,且A点到MN的距离是
 米.假设拖拉机行驶时,周围100米以内会受到噪声的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到噪声影响?说明理由;如果受影响,已知拖拉机的速度为18千米/时,那么学校受影响的时间为多少秒?
米.假设拖拉机行驶时,周围100米以内会受到噪声的影响,那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到噪声影响?说明理由;如果受影响,已知拖拉机的速度为18千米/时,那么学校受影响的时间为多少秒?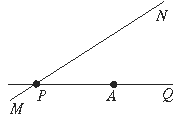
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OA=OB,OC=OD,AD和BC相交于点E,则图中共有全等三角形的对数( )

A. 2对 B. 3对 C. 4对 D. 5对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD⊥AB于点D,点E在CD上,下列四个条件:①AD=ED;②∠A=∠BED;③∠C=∠B;④AC=EB,将其中两个作为条件,不能判定△ADC≌△EDB的是
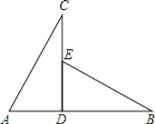
A.①②B.①④C.②③D.②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,二次函数
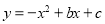 的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).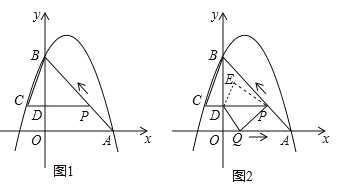
(1)求二次函数
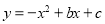 的表达式;
的表达式;(2)连接 BC ,当t=
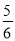 时,求△BCP的面积;
时,求△BCP的面积;(3)如图 2,动点 P 从 A 出发时,动点 Q 同时从 O 出发,在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动,当点 P 与 B 重合时,P 、 Q 两点同时停止运动,连接 DQ 、 PQ ,将△DPQ沿直线 PC 折叠到 △DPE .在运动过程中,设 △DPE 和 △OAB重合部分的面积为 S ,直接写出 S 与 t 的函数关系式及 t 的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用
 ,
, 表示直角三角形的两直角边(
表示直角三角形的两直角边( ),下列四个说法:
),下列四个说法:
①
 ,②
,② ,③
,③ ,④
,④ .
.其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ADC=90°,AD=8m,CD=6m,BC=24m,AB=26m,则图中阴影部分的面积为_________;

相关试题

