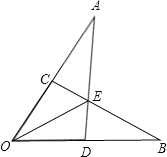
【题目】如图,已知OA=OB,OC=OD,AD和BC相交于点E,则图中共有全等三角形的对数( )

A. 2对 B. 3对 C. 4对 D. 5对
参考答案:
【答案】C
【解析】
由条件可证△AOD≌△BOC,可得∠A=∠B,则可证明△ACE≌△BDE,可得AE=BE,则可证明△AOE≌△BOE,可得∠COE=∠DOE,可证△COE≌△DOE,可求得答案.
解:
在△AOD和△BOC中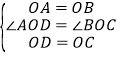
∴△AOD≌△BOC(SAS),
∴∠A=∠B,
∵OC=OD,OA=OB,
∴AC=BD,
在△ACE和△BDE中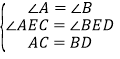
∴△ACE≌△BDE(AAS),
∴AE=BE,
在△AOE和△BOE中
∴△AOE≌△BOE(SAS),
∴∠COE=∠DOE,
在△COE和△DOE中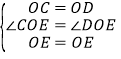
∴△COE≌△DOE(SAS),
故全等的三角形有4对,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场在一楼与二楼之间装有一部自动扶梯,以均匀的速度向上行驶,一男孩与一女孩同时从自动扶梯上走到二楼(扶梯本身也在行驶).如果二人都做匀速运动,且男孩每分钟走动的级数是女孩的两倍.又已知男孩走了27级到达顶部,女孩走了18级到达顶部(二人每步都只跨1级).求扶梯有多少级?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠CAB=∠DBA,添加下列某条件,未必能判定△ABC≌BAD的是( )
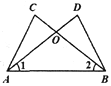
A. AC=BD B. AD=BC C. ∠l=∠2 D. ∠C=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】设边长为3的正方形的对角线长为a.下列关于a的四种说法: ①a是无理数;
②a可以用数轴上的一个点来表示;
③3<a<4;
④a是18的算术平方根.
其中,所有正确说法的序号是( )
A.①④
B.②③
C.①②④
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四个数:a=
 b=- (-3) , c= -(-1)2019, d=
b=- (-3) , c= -(-1)2019, d= .
.(1) 化简a,b,c,d 得a= ,b= ,c= ,d= ;
(2) 把这四个数在数轴上分别表示出来:

(3)用“<”把 a,b,c,d 连接起来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A、B、C、D是坐标轴上的点且点C坐标是(0,﹣1),AB=5,点(a,b)在如图所示的阴影部分内部(不包括边界),已知OA=OD=4,则a的取值范围是( )
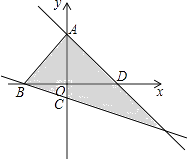
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=
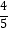 ,反比例函数y=
,反比例函数y= 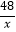 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( ) 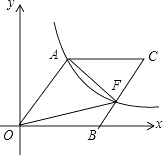
A.60
B.80
C.30
D.40
相关试题

