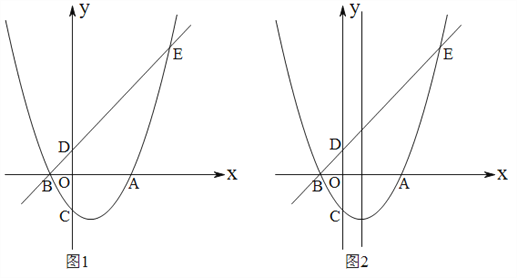
【题目】已知,如图1:抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,对称轴为直线
,对称轴为直线![]() ,且过点
,且过点![]() .
.
(1)求出抛物线的解析式及![]() 点坐标,
点坐标,
(2)点![]() ,
, ![]() ,作直线
,作直线![]() 交抛物线于另一点
交抛物线于另一点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的点,连接
下方抛物线上的点,连接![]() 、
、![]() ,求
,求![]() 的面积的最大值,并求出此时点
的面积的最大值,并求出此时点![]() 的坐标;
的坐标;
(3)点![]() 、
、![]() 是抛物线对称轴上的两点,且已知
是抛物线对称轴上的两点,且已知![]() (
(![]() ,
, ![]() ),
),![]() (
(![]() ,
, ![]() ),当
),当![]() 为何值时,四边形
为何值时,四边形![]() 周长最小?并求出四边形
周长最小?并求出四边形![]() 周长的最小值,请说明理由.
周长的最小值,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,
, ![]() ;(3)
;(3)![]() ,周长最小值是
,周长最小值是![]() ,理由见解析
,理由见解析
【解析】试题分析:(1)根据函数图象过点![]() 和对称轴方程列出方程组求解即可;
和对称轴方程列出方程组求解即可;
(2)求出点B的坐标,再求出直线BD的解析式,与抛物线联立方程组即可求出点E坐标,根据三角形面积的计算公式得出表示三角形面积的二次函数,求出最大值即可;
(3)在四边形ANME中,MN,AE是定值,四边形![]() 周长最小,即AN+ME最小.利用轴对称即可求解.
周长最小,即AN+ME最小.利用轴对称即可求解.
试题解析:(1)由题可得:

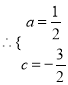
![]()
![]()
(2)当y=0时, ![]()
∴![]()
∴A(3,0),B(-1,0)
∵D(0,1)
∴直线BD:y=x+1
∴解方程![]() 得:
得: ![]()
∴E(5,6)
过点F作FG⊥x轴交直线BE于点G
设F(m, ![]() ),-1<m<5,G(m,m+1)
),-1<m<5,G(m,m+1)
∴GF=![]()
∴SΔDEF=![]()
∵![]() <0
<0
∴i当m=2时,ΔDEF的面积有最大值,最大值是![]()
∴F(2, ![]() )
)

(3)∵A(3,0),E(5,6)
∴AE=![]()
∵M(1,a+2),N(1,a)
∴MN=2
∴当ME+AN的值最小时,四边形AEMN的周长最小,
∵点![]() 和点B关于直线x=1对称,将点
和点B关于直线x=1对称,将点![]() 向下平移2个单位长度得到点
向下平移2个单位长度得到点![]() ,
,
连结BE交直线x=1于点N,再将点N向上平移2个单位长度得到点M,连结AN、ME、AE.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在①(-1)-3=1;②(-1)3=-3;③3a-2=
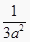 ;④(-x)5÷(-x)-2=-x7中,不正确的式子有( )
;④(-x)5÷(-x)-2=-x7中,不正确的式子有( )
A.①②
B.②③
C.①②③
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程变形正确的是( )
A.方程3x﹣2=2x﹣1移项,得3x﹣2x=﹣1﹣2
B.方程3﹣x=2﹣5(x﹣1)去括号,得3﹣x=2﹣5x﹣1
C.方程 可化为3x=6.
可化为3x=6.
D.方程 系数化为1,得x=﹣1
系数化为1,得x=﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】六一期间,某公园游戏场举行“迎奥运”活动.有一种游戏的规则是:在一个装有6个红球和若干个白球(每个球除颜色外其他相同)的袋中,随机摸一个球,摸到一个红球就得到一个奥运福娃玩具.已知参加这种游戏活动为40000人次,公园游戏场发放的福娃玩具为10000个.
(1)求参加一次这种游戏活动得到福娃玩具的概率;
(2)请你估计袋中白球接近多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】从一副扑克牌中抽出3张红桃,4张梅花,3张黑桃放在一起洗匀后,从中一次随机抽出8张,恰好红桃、梅花、黑桃3种牌都抽到,这件事件( )
A.可能发生 B.不可能发生 C.很可能发生 D.必然发生
-
科目: 来源: 题型:
查看答案和解析>>【题目】按下面的程序计算:

当输入 x=100 时,输出结果是299;当输入 x=50 时,输出结果是446;如果输入 x 的值是正整数,输出结果是257,那么满足条件的 x 的值最多有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并将解集在数轴上表示出来.
,并将解集在数轴上表示出来.
相关试题

