搜索
【题目】下表是某水库一周内水位高低的变化情况(用正数记水位比前一日上升数，用负数记下降数)．那么本周星期几水位最低 （ ）
A. 星期二B. 星期四C. 星期六D. 星期五
参考答案：
【答案】C
【解析】
把周一之前的水位看作0，计算七天水位，比较得出答案即可．
把周一之前的水位看作0，
第一天水位：0.12米，
第二天水位：0.12-0.02=0.1米，
第三天水位：0.1-0.13=-0.03米，
第四天水位：-0.03-0.20=-0.23米，
第五天水位：-0.23-0.08=-0.31米，
第六天水位：-0.31-0.02=-0.33米，
第七天水位：-0.33+3.12=-0.01米，
周一水位最高，周六水位最低，高0.12-（-0.33）=0.45米．
故选C.
-
科目： 来源： 题型：
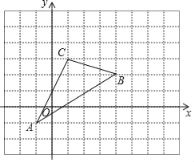
查看答案和解析>>【题目】如图，三角形ABC在直角坐标系中．
（1）请直接写出点A、C两点的坐标：
（2）三角形ABC的面积是 ；
（3）若把三角形ABC向上平移1个单位，再向右平移1个单位得三角形A′B′C′在图中画出三角形A′B′C’，这时点B′的坐标为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，
，点
是直线
、
之间的一点，连接
、
.（1）探究猜想：
①若
，则
.②若
，则 .③猜想图1中
、
、
的关系，并证明你的结论.（2）拓展应用：
如图2，
，线段
把
这个封闭区域分为I、II两部分（不含边界），点是位于这两个区域内的任意一点，请直接写出
、
、
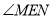的关系.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，E，F分别是AD，BC边上的点，AE＝CF，∠EFB＝45°，若AB＝5，BC＝13，则AE的长为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y＝－
x2＋
x－2与x轴相交于点A、B，与y轴相交于点C.（1）求证：△AOC∽△COB；
（2）过点C作CD∥x轴交抛物线于点D．若点P在线段AB上以每秒1个单位的速度由A向B运动，同时点Q在线段CD上也以每秒1个单位的速度由D向C运动，则经过几秒后，PQ＝AC.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：线段AB，BC．
求作：平行四边形ABCD．
以下是甲、乙两同学的作业．
甲：
①以点C为圆心，AB长为半径作弧；
②以点A为圆心，BC长为半径作弧；
③两弧在BC上方交于点D，连接AD，CD．
四边形ABCD即为所求平行四边形．（如图1）
乙：
①连接AC，作线段AC的垂直平分线，交AC于点M；
②连接BM并延长，在延长线上取一点D，使MD=MB，连接AD，CD．
四边形ABCD即为所求平行四边形．（如图2）
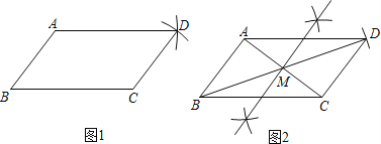
老师说甲、乙同学的作图都正确，你更喜欢______的作法，他的作图依据是：______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程
已知：直线l及直线l外一点P．
求作：直线PQ，使得PQ∥l．
作法：如图，
①在直线l上取一点A，作射线AP，以点P为圆心，PA长为半径画弧，交AP的
延长线于点B；
②以点B为圆心，BA长为半径画弧，交l于点C（不与点A重合），连接BC；
③以点B为圆心，BP长为半径画孤，交BC于点Q；
④作直线PQ．
所以直线PQ就是所求作的直线．
根据小东设计的尺规作图过程，
（1）使用直尺和圆规，补全图形；（保留作图痕迹）
（2）完成下面的证明
证明：∵PB＝PA，BC＝ ，BQ＝PB，
∴PB＝PA＝BQ＝ ．
∴PQ∥l（ ）（填推理的依据）．
相关试题
