【题目】如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°
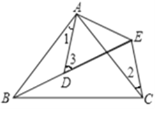
(1)求证△ABD≌△ACE
(2)求∠3度数.
参考答案:
【答案】(1)见解析;(2)51°.
【解析】
根据∠BAC=∠DAE通过角的计算即可得出∠1=∠CAE,结合AB=AC、AD=AE即可证出△BAD≌△CAE(SAS),进而即可得出∠ABD=∠2=30°.再根据外角的性质即可得出∠3的度数.
(1)∵∠BAC=∠DAE,∠BAC=∠1+∠DAC,∠DAE=∠DAC+∠CAE,
∴∠1=∠CAE.
在△ABD和△ACE中,
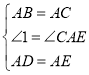 ,
,
∴△ABD≌△ACE (SAS),
(2) ∴∠ABD=∠2=30°.
∵∠3=∠1+∠ABD=21°+30°=51°,
故答案为:51°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=5,∠B=∠C,BC=8,点D从B点出发沿线段BC向C运动(D不与B、C重合),点E从点C出发沿线段CA向A运动(E不与A、C重合),它们以相同的速度同时运动,连结AD、DE.若要使△ABD≌△DCE,①请给出确定D、E两点位置的方法(如指明CD长度等),并说明理由;②此时∠ADE与∠C大小关系怎样?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:O是直线AB上的一点,
 是直角,OE平分
是直角,OE平分 .
.(1)如图1.若
 .求
.求 的度数;
的度数;(2)在图1中,
 ,直接写出
,直接写出 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);(3)将图1中的
 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究 和
和 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )

A.35°B.40°C.45°D.50°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠AOB=125°,把△ABC剪成三部分,边AB、BCAC放在同一直线上,点O都落在直线MN上,且S△BCO:S△CAO:S△ABO=BC:CA:AB,则∠ACB的度数为( )
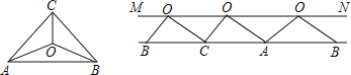
A.70°B.65°C.60°D.85°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数的图像经过点A(0,4) ,且与两坐标轴围成的三角形面积是8,则这个函数的解析式是( )
A.
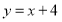 或
或 B.
B. 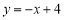 或
或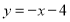
C.
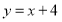 或
或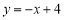 D.
D.  或
或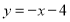
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数 y=kx+b 的图象经过点(-1,-5),且与正比例函数
 于点(2,a),求:
于点(2,a),求:(1)a 的值;
(2)k,b 的值;
(3)这两个函数图象与 x 轴所围成的三角形的面积.
相关试题

