【题目】解方程:
(1)3x(x﹣1)=2x﹣2
(2)x2﹣6x+5=0(配方法)
参考答案:
【答案】
(1)解:∵3x(x﹣1)=2(x﹣1),
∴3x(x﹣1)﹣2(x﹣1)=0,即(x﹣1)(3x﹣2)=0,
∴x﹣1=0或3x﹣2=0,
解得:x=1或x= ![]()
(2)解:∵x2﹣6x=﹣5,
∴x2﹣6x+9=﹣5+9,即(x﹣3)2=4,
∴x﹣3=2或x﹣3=﹣2,
解得:x=5或x=1
【解析】(1)因式分解法求解可得;(2)配方法求解可得.
【考点精析】通过灵活运用配方法和因式分解法,掌握左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题;已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,AB=8,BC=4.在AD上取一点E,AE=1,点F是AB边上的一个动点,以EF为一边作菱形EFMN,使点N落在CD边上,点M落在矩形ABCD内或其边上.若AF=x,△BFM的面积为S.
(1)当四边形EFMN是正方形时,求x的值;

(2)当四边形EFMN是菱形时,求S与x的函数关系式;

(3)当x= 时,△BFM的面积S最大;当x= 时,△BFM的面积S最小;
(4)在△BFM的面积S由最大变为最小的过程中,请直接写出点M运动的路线长: 。


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△BDE中,∠BDE=90°,BD=6
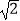 ,点D的坐标是(7,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 .
,点D的坐标是(7,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 . 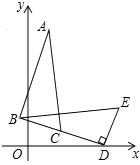
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,以点A为圆心,小于AC的长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,以大于
 EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )
EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )
A. 120° B. 30° C. 150° D. 60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABC=∠DCB,添加一个条件,使△ABC≌△DCB,你添加的条件是_____.(注:只需写出一个条件即可)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
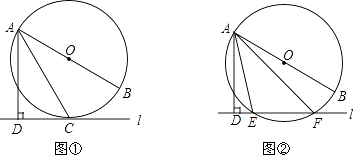
(1)如图①,当直线l与⊙O相切于点C时,求证:AC平分∠DAB;
(2)如图②,当直线l与⊙O相交于点E,F时,求证:∠DAE=∠BAF.
相关试题

