【题目】已知:如图,在矩形ABCD中,AB=8,BC=4.在AD上取一点E,AE=1,点F是AB边上的一个动点,以EF为一边作菱形EFMN,使点N落在CD边上,点M落在矩形ABCD内或其边上.若AF=x,△BFM的面积为S.
(1)当四边形EFMN是正方形时,求x的值;

(2)当四边形EFMN是菱形时,求S与x的函数关系式;

(3)当x= 时,△BFM的面积S最大;当x= 时,△BFM的面积S最小;
(4)在△BFM的面积S由最大变为最小的过程中,请直接写出点M运动的路线长: 。


参考答案:
【答案】(1)x=3;(2)S=![]() ;(3)
;(3)![]() ;(4)
;(4) ![]()
【解析】
(1)利用AAS证明△DEN≌△AFE即可解决问题;
(2)如图,过点M作MH⊥AB于H,连接NF,证明△DEN≌△HMF,可得MH=DE=3,由此即可解决问题;
(3)①如备用图①中,当点N与点D重合时,x的值最小,△FBM的面积最大,在Rt△AEF中,x=![]() ,推出S的最大值=12-3
,推出S的最大值=12-3![]() ;②如备用图②,当点M在BC上时,x的值最大,△FBM的面积最小;
;②如备用图②,当点M在BC上时,x的值最大,△FBM的面积最小;
(4)如备用图③中,在△BFM的面积S由最大变为最小的过程中,点M的运动轨迹是平行AB的线段,点M运动的路线长=BF的长=8-2![]() .
.
(1)在正方形EFMN中,∠FEN=90°,EF=EN,
∴ ∠DEN+∠AEF=90°,
在矩形ABCD中,∠A=∠D=90°,
∴ ∠AEF+∠AFE=90°,
∴ ∠DEN=∠AFE,
在△DEN与△AFE中,
 ,
,
∴△DEN≌△AFE(AAS),
∴AF=DE=4-1=3,
∴x的值为3;
(2)过点M作MH⊥AB于H,连接NF,
在矩形ABCD中,∵AB∥CD,
∴∠DNF=∠NFB,
∵四边形EFMN是菱形,
∴NE‖MF ,NE=MF,
∴∠ENF=∠MFN,
∴∠DNE=∠MFB ,
在△DEN与△HMF中,
 ,
,
∴△DEN≌△HMF(AAS),
∴MH=DE=3,BF=8-x,
![]() ;
;

(3)①如备用图①中,当点N与点D重合时,x的值最小,△FBM的面积最大,
在Rt△AEF中,x=![]() ,
,
∴S的最大值=12-3![]() ;
;
②如备用图②,当点M在BC上时,x的值最大,△FBM的面积最小,
此时易得CN=AF=x,
∵EN=EF,
∴12+x2=32+(8-x)2,
∴x=![]() ,
,
∴S的最小值为![]() ,
,
故答案为:2![]() ,
,![]() ;
;
(4)如备用图③中,在△BFM的面积S由最大变为最小的过程中,点M的运动轨迹是平行AB的线段,点M运动的路线长=BF的长=8-2![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
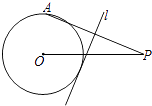
查看答案和解析>>【题目】如图,⊙O的半径为4,点P是⊙O外的一点,PO=10,点A是⊙O上的一个动点,连接PA,直线l垂直平分PA,当直线l与⊙O相切时,PA的长度为( )
A.10
B.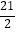
C.11
D.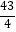
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论: ①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )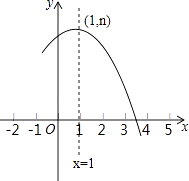
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=x+1与x、y 轴分别交于点A、B,在直线 AB上截取BB1=AB,过点B1分别作x、y 轴的垂线,垂足分别为点A1、C1,得到矩形OA1B1C1;在直线 AB上截取B1B2= BB1,过点B2分别作x、y 轴的垂线,垂足分别为点A2 、C2,得到矩形OA2B2C2;在直线AB上截取B2B3= B1B2,过点B3分别作x、y 轴的垂线,垂足分别为点A3、C3,得到矩形OA3B3C3;……;
则点B1的坐标是 ;第3个矩形OA3B3C3的面积是 ;
第n个矩形OAnBnCn的面积是 (用含n的式子表示,n是正整数).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△BDE中,∠BDE=90°,BD=6
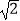 ,点D的坐标是(7,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 .
,点D的坐标是(7,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 . 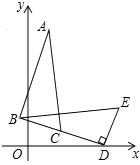
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,以点A为圆心,小于AC的长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,以大于
 EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )
EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )
A. 120° B. 30° C. 150° D. 60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)3x(x﹣1)=2x﹣2
(2)x2﹣6x+5=0(配方法)
相关试题

