【题目】如图,在△BDE中,∠BDE=90°,BD=6 ![]() ,点D的坐标是(7,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 .
,点D的坐标是(7,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 . 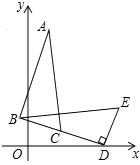
参考答案:
【答案】(4,3 ![]() )
)
【解析】解:如图,AB与BD的垂直平分线的交点即为旋转中心P, 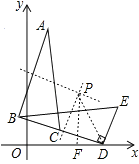 连接PD,过P作PF⊥x轴于F,
连接PD,过P作PF⊥x轴于F,
∵点C在BD上,
∴点P到AB、BD的距离相等,都是 ![]() BD,即
BD,即 ![]() ×6
×6 ![]() =3
=3 ![]() ,
,
∴∠PDB=45°,
PD=3 ![]() ×
× ![]() =6,
=6,
∵∠BDO=15°,
∴∠PDO=45°+15°=60°,
∴∠DPF=30°,
∴DF= ![]() PD=
PD= ![]() ×6=3,
×6=3,
∵点D的坐标是(7,0),
∴OF=OD﹣DF=7﹣3=4,
由勾股定理得,PF= ![]() =
= ![]() =3
=3 ![]() ,
,
即P点的坐标为(4,3 ![]() ),
),
故答案为:(4,3 ![]() ).
).
根据旋转的性质,AB与BD的垂直平分线的交点即为旋转中心P,连接PD,过P作PF⊥x轴于F,再根据点C在BD上确定出∠PDB=45°并求出PD的长,然后求出∠PDO=60°,根据直角三角形两锐角互余求出∠DPF=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得DF= ![]() PD,利用勾股定理列式求出PF,再求出OF,即可得到点P,即旋转中心的坐标.
PD,利用勾股定理列式求出PF,再求出OF,即可得到点P,即旋转中心的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论: ①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )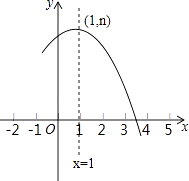
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=x+1与x、y 轴分别交于点A、B,在直线 AB上截取BB1=AB,过点B1分别作x、y 轴的垂线,垂足分别为点A1、C1,得到矩形OA1B1C1;在直线 AB上截取B1B2= BB1,过点B2分别作x、y 轴的垂线,垂足分别为点A2 、C2,得到矩形OA2B2C2;在直线AB上截取B2B3= B1B2,过点B3分别作x、y 轴的垂线,垂足分别为点A3、C3,得到矩形OA3B3C3;……;
则点B1的坐标是 ;第3个矩形OA3B3C3的面积是 ;
第n个矩形OAnBnCn的面积是 (用含n的式子表示,n是正整数).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,AB=8,BC=4.在AD上取一点E,AE=1,点F是AB边上的一个动点,以EF为一边作菱形EFMN,使点N落在CD边上,点M落在矩形ABCD内或其边上.若AF=x,△BFM的面积为S.
(1)当四边形EFMN是正方形时,求x的值;

(2)当四边形EFMN是菱形时,求S与x的函数关系式;

(3)当x= 时,△BFM的面积S最大;当x= 时,△BFM的面积S最小;
(4)在△BFM的面积S由最大变为最小的过程中,请直接写出点M运动的路线长: 。


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,以点A为圆心,小于AC的长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,以大于
 EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )
EF长为半径作圆弧,两条弧交于点G,作射线AG交CD于点H,若∠C=120°,则∠AHD=( )
A. 120° B. 30° C. 150° D. 60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)3x(x﹣1)=2x﹣2
(2)x2﹣6x+5=0(配方法) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
相关试题

