Question

【题目】已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D．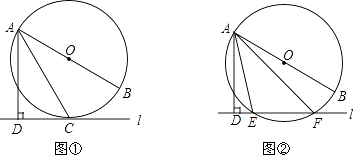
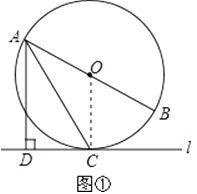
（1）如图①，当直线l与⊙O相切于点C时，求证：AC平分∠DAB；
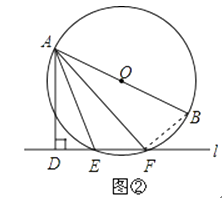
（2）如图②，当直线l与⊙O相交于点E，F时，求证：∠DAE=∠BAF．

Answer 1

【答案】
（1）解：连接OC，

∵直线l与⊙O相切于点C，

∴OC⊥CD；

又∵AD⊥CD，

∴AD∥OC，

∴∠DAC=∠ACO；

又∵OA=OC，

∴∠ACO=∠CAO，

∴∠DAC=∠CAO，

即AC平分∠DAB

（2）解：如图②，连接BF，

∵AB是⊙O的直径，

∴∠AFB=90°，

∴∠BAF=90°﹣∠B，

∴∠AEF=∠ADE+∠DAE，

在⊙O中，四边形ABFE是圆的内接四边形，

∴∠AEF+∠B=180°，

∴∠BAF=∠DAE．

【解析】（1）连接OC，易得OC∥AD，根据平行线的性质就可以得到∠DAC=∠ACO，再根据OA=OC得到∠ACO=∠CAO，就可以证出结论；（2）如图②，连接BF，由AB是⊙O的直径，根据直径所对的圆周角是直角，可得∠AFB=90°，由三角形外角的性质，可求得∠AEF的度数，又由圆的内接四边形的性质，继而证得结论．