【题目】问题发现:如图1,在△ABC中,∠C=90°,分别以AC、BC为边向外侧作正方形ACDE和正方形BCFG.
(1)△ABC与△DCF面积的关系是;(请在横线上填写“相等”或“不相等”)
(2)拓展探究:若∠C≠90°,(1)中的结论还成立吗?若成立,请结合图2给出证明;若不成立,请说明理由;
(3)解决问题:如图3,在四边形ABCD中,AC⊥BD,且AC与BD的和为10,分别以四边形ABCD的四条边为边向外侧作正方形ABFE、正方形BCHG、正方形CDJI、正方形DALK,运用(2)的结论,图中阴影部分的面积和是否有最大值?如果有,请求出最大值,如果没有,请说明理由.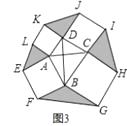
参考答案:
【答案】
(1)相等
(2)解:成立.理由如下:
延长BC到点P,过点A作AP⊥BP于点P;过点D作DQ⊥FC于点Q.如图所示:
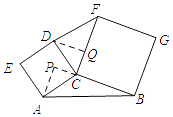
∴∠APC=∠DQC=90°.
∵四边形ACDE,BCFG均为正方形,
∴AC=CD,BC=CF,∠ACP+∠PCD=90°,∠DCQ+∠PCD=90°,
∴∠ACP=∠DCQ.
在△APC和△DQC中, 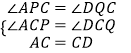 ,
,
△APC≌△DQC(AAS),
∴AP=DQ.
又∵S△ABC= ![]() BCAP,S△DFC=
BCAP,S△DFC= ![]() FCDQ,
FCDQ,
∴S△ABC=S△DFC;
(3)解:图中阴影部分的面积和有最大值,理由如下:
由(2)得:S△AEL=S△ABD,S△BFG=S△ABC,S△CIH=S△CBD,S△DLK=S△DAC,
∴阴影部分的面和S=S△AEL+S△BFG+S△CIH+S△DLK=2S四边形ABCD,
设AC=x,则BD=10﹣x,
∵AC⊥BD,
∴S四边形ABCD= ![]() AC×BD=
AC×BD= ![]() x(10﹣x)=﹣
x(10﹣x)=﹣ ![]() x2+5x=﹣
x2+5x=﹣ ![]() (x﹣5)2+
(x﹣5)2+ ![]() ,
,
∵﹣ ![]() <0,
<0,
∴S四边形ABCD有最大值,最大值为 ![]() ,
,
∴图中阴影部分的面积和有最大值为25.
【解析】解:(1)相等;理由如下:
∵四边形ACDE和四边形BCFG是正方形,
∴AC=DC,BC=FC,∠ACD=∠BCF=90°,
∵∠ACB=90°,
∴∠DCF=90°=∠ACB;
在△ABC与△DFC中, 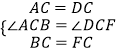 ,
,
∴△ABC≌△DFC(AAS).
∴△ABC与△DFC的面积相等;
所以答案是:相等;
【考点精析】本题主要考查了二次函数的最值的相关知识点,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
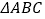 的
的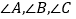 所对边分别是
所对边分别是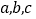 ,且
,且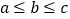 ,若满足
,若满足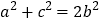 ,则称
,则称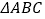 为奇异三角形,例如等边三角形就是奇异三角形.
为奇异三角形,例如等边三角形就是奇异三角形.(1)若
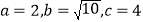 ,判断
,判断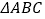 是否为奇异三角形,并说明理由;
是否为奇异三角形,并说明理由;(2)若
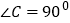 ,
,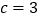 ,求
,求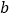 的长;
的长;(3)如图2,在奇异三角形
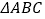 中,
中,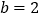 ,点
,点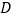 是
是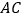 边上的中点,连结
边上的中点,连结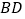 ,
,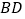 将
将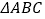 分割成2个三角形,其中
分割成2个三角形,其中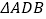 是奇异三角形,
是奇异三角形,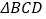 是以
是以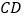 为底的等腰三角形,求
为底的等腰三角形,求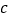 的长.
的长.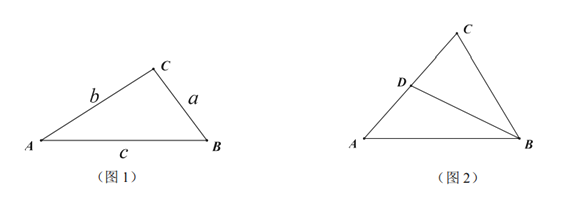
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,∠1=∠2,CF平分∠DCE.
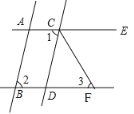
(1)试判断直线AE与BF有怎样的位置关系,并说明理由;
(2)若∠1=80°,求∠3的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 ,
, ,过点
,过点 画
画 轴的垂线
轴的垂线 ,点
,点 在线段
在线段 上,连结
上,连结 并延长交直线
并延长交直线 于点
于点 ,过点
,过点 画
画 交直线
交直线 于点
于点 .
.(1)求
 的度数,并直接写出直线
的度数,并直接写出直线 的解析式;
的解析式;(2)若点
 的横坐标为2,求
的横坐标为2,求 的长;
的长;(3)当
 时,求点
时,求点 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下面的解答过程补充完整:如图,点
 在
在 上,点
上,点 在
在 上,
上, ,
, .试说明:
.试说明: ∥
∥ .
.
解:∵
 (已知)
(已知) ( )
( )∴
 (等量代换)
(等量代换)∴ ______∥_______( )
∴
 ( )
( )∵
 (已知)
(已知)∴
 ( )
( )∴
 ∥
∥ ( )
( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,且AN=8,BN=6,AC=16,则MN的长是()

A. 4B. 3C. 2.5D. 2
相关试题

