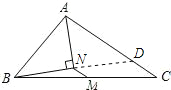
【题目】如图,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,且AN=8,BN=6,AC=16,则MN的长是()

A. 4B. 3C. 2.5D. 2
参考答案:
【答案】B
【解析】
由勾股定理得AB=10,延长BN交AC于D,易得△ABN≌△ADN,则全等三角形的对应边相等:AD=AB=10,点N是BD的中点,MN是△BCD的CD边对的中位线,故有MN=![]() CD.
CD.
解:如图,延长BN交AC于D.
Rt△ABN中,∵AN=8,BN=6,∴AB=10
∵AN平分∠BAC
∴∠BAN=∠DAN,
∵BN⊥AN
∴∠ANB=∠AND,
在△ABN和△ADN中,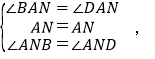
∴△ABN≌△ADN(ASA)
∴BN=DN,AD=AB=10,DN=NB,
∴CD=AC-AD=16-10=6,
又∵点M是BC中点,
∴MN是△BDC的中位线,
∴MN=![]() CD=
CD=![]() (AC-AD)=3.
(AC-AD)=3.
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题发现:如图1,在△ABC中,∠C=90°,分别以AC、BC为边向外侧作正方形ACDE和正方形BCFG.

(1)△ABC与△DCF面积的关系是;(请在横线上填写“相等”或“不相等”)
(2)拓展探究:若∠C≠90°,(1)中的结论还成立吗?若成立,请结合图2给出证明;若不成立,请说明理由;
(3)解决问题:如图3,在四边形ABCD中,AC⊥BD,且AC与BD的和为10,分别以四边形ABCD的四条边为边向外侧作正方形ABFE、正方形BCHG、正方形CDJI、正方形DALK,运用(2)的结论,图中阴影部分的面积和是否有最大值?如果有,请求出最大值,如果没有,请说明理由.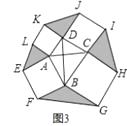
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 ,
, ,过点
,过点 画
画 轴的垂线
轴的垂线 ,点
,点 在线段
在线段 上,连结
上,连结 并延长交直线
并延长交直线 于点
于点 ,过点
,过点 画
画 交直线
交直线 于点
于点 .
.(1)求
 的度数,并直接写出直线
的度数,并直接写出直线 的解析式;
的解析式;(2)若点
 的横坐标为2,求
的横坐标为2,求 的长;
的长;(3)当
 时,求点
时,求点 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下面的解答过程补充完整:如图,点
 在
在 上,点
上,点 在
在 上,
上, ,
, .试说明:
.试说明: ∥
∥ .
.
解:∵
 (已知)
(已知) ( )
( )∴
 (等量代换)
(等量代换)∴ ______∥_______( )
∴
 ( )
( )∵
 (已知)
(已知)∴
 ( )
( )∴
 ∥
∥ ( )
( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
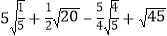 ;
; (2)
 ;
; (3)
 ;
;(4)先化简,再求值:(
 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形ABC(记作△ABC)在8×8方格中,位置如图所示,A(-3,1),B(-2,4).

(1)请你在方格中建立直角坐标系,并写出C点的坐标;
(2)把△ABC向下平移1个单位长度,再向右平移2个单位长度,请你画出平移后的△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是 .
(3)在x轴上存在一点D,使△DB1C1的面积等于3,求满足条件的点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=ax2+bx+
 经过A(1,0),B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边三角形ABC.
经过A(1,0),B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边三角形ABC.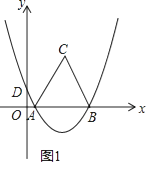
(1)求抛物线的解析式;
(2)在x轴上方的抛物线上是否存在点M,是S△ABM=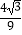 S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)如图2,E是线段AC上的动点,F是线段BC上的动点,AF与BE相交于点P.
①若CE=BF,试猜想AF与BE的数量关系及∠APB的度数,并说明理由;
②若AF=BE,当点E由A运动到C时,请直接写出点P经过的路径长.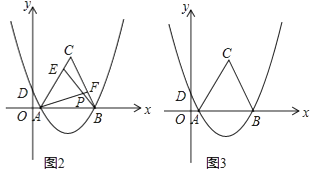
相关试题

