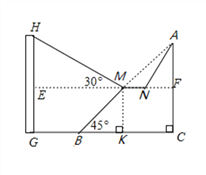
【题目】市政府对城市建设进行了整改,如图,已知斜坡AB长![]() 米,坡角(即∠ABC)为45°,AC⊥BC,现计划在斜坡中点M处挖去部分斜坡,修建一个平行于水平线CB的休闲平台MN和一条新的斜坡AN.(温馨提示:后两个小题结果都保留根号)
米,坡角(即∠ABC)为45°,AC⊥BC,现计划在斜坡中点M处挖去部分斜坡,修建一个平行于水平线CB的休闲平台MN和一条新的斜坡AN.(温馨提示:后两个小题结果都保留根号)
(1)若修建的斜坡AN的坡比为![]() ,求休闲平台MN的长是多少米?
,求休闲平台MN的长是多少米?
(2)一座建筑物GH距离B点34米远(BG=34米),小亮在M点测得建筑物顶部H的仰角(即∠HME)为30°.点A、C、B、G,H在同一个平面内,点C、B、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() 米.
米.
【解析】分析:(1)由三角函数的定义,即可求得AM与AF的长,又由坡度的定义,即可求得NF的长,继而求得平台MN的长;(2)在RT△BMK中,求得BK=MK=50米,从而求得 EM=84米;在RT△HEM中, 求得![]() ,继而求得
,继而求得![]() 米.
米.
详解:
(1)∵MF∥BC,∴∠AMF=∠ABC=45°,
∵斜坡AB长![]() 米,M是AB的中点,∴AM=
米,M是AB的中点,∴AM=![]() (米),
(米),
∴AF=MF=AMcos∠AMF=![]() (米),
(米),
在![]() 中,∵斜坡AN的坡比为
中,∵斜坡AN的坡比为![]() ∶1,∴
∶1,∴![]() ,
,
∴![]() ,
,
∴MN=MF-NF=50-![]() =
=![]() .
.
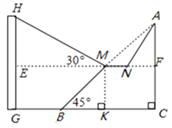
(2)在RT△BMK中,BM=![]() ,∴BK=MK=50(米),
,∴BK=MK=50(米),
EM=BG+BK=34+50=84(米)
在RT△HEM中,∠HME=30°,∴![]() ,
,
∴![]() ,
,
∴![]() (米)
(米)
答:休闲平台DE的长是![]() 米;建筑物GH高为
米;建筑物GH高为![]() 米.
米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简与求值
(1)求3x2+x+3(x2﹣
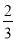 x)﹣(6x2+x)的值,其中x=﹣6.
x)﹣(6x2+x)的值,其中x=﹣6.(2)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中|a+1|+(b﹣
 )2=0
)2=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】按要求画图,并解答问题
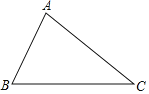
(1)如图,取BC边的中点D,画射线AD;
(2)分别过点B、C画BE⊥AD于点E,CF⊥AD于点F;
(3)BE和CF的位置关系是 ;通过度量猜想BE和CF的数量关系是 .
-
科目: 来源: 题型:
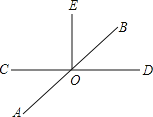
查看答案和解析>>【题目】已知:如图,直线AB、CD相交于点O,EO⊥CD于O.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,请你过点O画直线MN⊥AB,并在直线MN上取一点F(点F与O不重合),然后直接写出∠EOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年元旦期间,某商场打出促销广告,如表所示.
优惠
条件
一次性购物不超过200元
一次性购物超过200元,但不超过500元
一次性购物超过500元
优惠
办法
没有优惠
全部按九折优惠
其中500元仍按九折优惠,超过500元部分按八折优惠
小欣妈妈两次购物分别用了134元和490元.
(1)小欣妈妈这两次购物时,所购物品的原价分别为多少?
(2)若小欣妈妈将两次购买的物品一次全部买清,则她是更节省还是更浪费?说说你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线 y 2x 4 与 x 轴、 y 轴分别交于 A 、 B 两点.
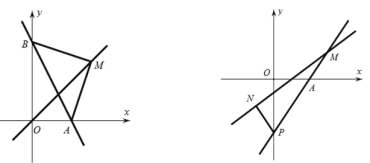
(1)求 A 、 B 两点的坐标;
(2)若点 M 为直线 y mx 上一点,且ABM 是等腰直角三角形,求 m 的值;
(3)过 A 点的直线 y kx 2k 交 y 轴负半轴于 P ,N 点的横坐标为1,过 N 点的直线
 于点 M ,试探究 PM 与 PN 之间的数量关系.
于点 M ,试探究 PM 与 PN 之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 是线段
是线段 上任一点,
上任一点, ,
, 两点分别从
两点分别从 同时向
同时向 点运动,且
点运动,且 点的运动速度为
点的运动速度为 ,
, 点的运动速度为
点的运动速度为 ,运动的时间为
,运动的时间为 .
.(1)若
 ,
,①运动
 后,求
后,求 的长;
的长;②当
 在线段
在线段 上运动时,试说明
上运动时,试说明 ;
;(2)如果
 时,
时, ,试探索
,试探索 的值.
的值.
相关试题

