【题目】按要求画图,并解答问题
(1)如图,取BC边的中点D,画射线AD;
(2)分别过点B、C画BE⊥AD于点E,CF⊥AD于点F;
(3)BE和CF的位置关系是 ;通过度量猜想BE和CF的数量关系是 .
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)BE∥CF,BE=CF.
【解析】
(1)根据中点的定义和射线的概念作图即可;
(2)根据垂线的概念作图即可得;
(3)根据平行线的判定以及全等三角形的判定与性质进行解答即可得.
解:(1)如图所示,射线AD即为所求;
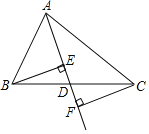
(2)如图所示BE、CF即为所求;
(3)由测量知BE∥CF且BE=CF,
∵BE⊥AD、CF⊥AD,
∴∠BED=∠CFD=90°,∴BE∥CF,
又∵∠BDE=∠CDF,BD=CD,
∴△BDE≌△CDF(AAS),
∴BE=CF,
故答案为:BE∥CF,BE=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在八年级举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查30名学生的听写汉字的正确字数如下:
2
9
17
24
33
5
12
19
26
34
7
14
20
26
36
15
22
26
39
31
22
27
39
22
28
23
23
31
30
28
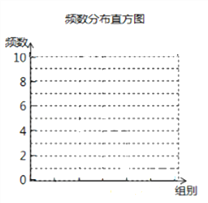
对这30个数据按组距8进行分组,并统计整理.
(1)请完成下面频数分布统计表;
组别
正确字数x
频数
A
0≤x<8
B
8≤x<16
C
16≤x<24
D
24≤x<32
E
32≤x<40
(2)在上图中请画出频数分布直方图;
(3)若该校八年级学生共有1200人,如果听写正确的个数少于24个定为不合格,请你估计该校八年级本次比赛听写不合格的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把所有正偶数从小到大排列,并按如下规律分组:(2)、(4,6),(8,10,12),(14,16,18,20),…,现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左往右数).如A2=(1,1),A10=(3,2),A18=(4,3),则A200可表示为( )
A.(14,9)B.(14,10)C.(15,9)D.(15,10)
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简与求值
(1)求3x2+x+3(x2﹣
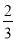 x)﹣(6x2+x)的值,其中x=﹣6.
x)﹣(6x2+x)的值,其中x=﹣6.(2)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中|a+1|+(b﹣
 )2=0
)2=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,直线AB、CD相交于点O,EO⊥CD于O.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,请你过点O画直线MN⊥AB,并在直线MN上取一点F(点F与O不重合),然后直接写出∠EOF的度数.
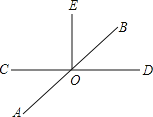
-
科目: 来源: 题型:
查看答案和解析>>【题目】市政府对城市建设进行了整改,如图,已知斜坡AB长
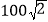 米,坡角(即∠ABC)为45°,AC⊥BC,现计划在斜坡中点M处挖去部分斜坡,修建一个平行于水平线CB的休闲平台MN和一条新的斜坡AN.(温馨提示:后两个小题结果都保留根号)
米,坡角(即∠ABC)为45°,AC⊥BC,现计划在斜坡中点M处挖去部分斜坡,修建一个平行于水平线CB的休闲平台MN和一条新的斜坡AN.(温馨提示:后两个小题结果都保留根号)(1)若修建的斜坡AN的坡比为
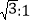 ,求休闲平台MN的长是多少米?
,求休闲平台MN的长是多少米?(2)一座建筑物GH距离B点34米远(BG=34米),小亮在M点测得建筑物顶部H的仰角(即∠HME)为30°.点A、C、B、G,H在同一个平面内,点C、B、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
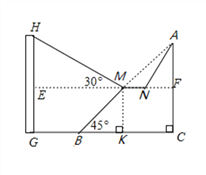
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年元旦期间,某商场打出促销广告,如表所示.
优惠
条件
一次性购物不超过200元
一次性购物超过200元,但不超过500元
一次性购物超过500元
优惠
办法
没有优惠
全部按九折优惠
其中500元仍按九折优惠,超过500元部分按八折优惠
小欣妈妈两次购物分别用了134元和490元.
(1)小欣妈妈这两次购物时,所购物品的原价分别为多少?
(2)若小欣妈妈将两次购买的物品一次全部买清,则她是更节省还是更浪费?说说你的理由.
相关试题

