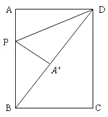
【题目】如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.

参考答案:
【答案】答案见解析
【解析】整体分析:
因为不确定△BPA′的哪一个角是直角,所以需要分三种情况讨论,即(1)当∠BA′P=90°时;(2)当∠A′PB=90°时;(3)当∠A′BP=90°时,注意画出符合各种情况的图形,找出折叠后相等的边和角.
解:(1)当∠BA′P=90°时,由折叠得,∠PA′D=∠A=90°,
∴∠BA′D=∠BA′P+∠PA′D=180°,
∴点B、A′、D在一直线上,
Rt△ABD中,AD=6,AB=8,由勾股定理得BD=10.
设AP=xcm,
∴A′P=x,BP=8-x,A′B=10-6=4,
在Rt△A′PB中,x2+42=(8-x)2,
解得x=3.
∴点P运动的时间为3÷1=3秒.
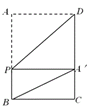
(2)当∠A′PB=90°时,∠A′PA=90°,
∵∠DA′P=90°,∴四边形APA′D是矩形,
∴A′P=AP,∴四边形APA′D是正方形,∴AP=AD=6,
∴点P运动的时间为6÷1=6秒.
(3)当∠A′BP=90°时,不存在.
综上所述,点P的运动时间为3s或6s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,AD∥BC,E为AB边上一点, ∠BCE=15°,EF∥AD交DC于点F.
(1)依题意补全图形,求∠FEC的度数;
(2)若∠A=140°,求∠AEC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系xOy的原点O在格点上,x轴、y轴都在格线上.线段AB的两个端点也在格点上.
(1)若将线段AB绕点O逆时针旋转90°得到线段A1B1,试在图中画出线段A1B1.
(2)若线段A2B2与线段A1B1关于y轴对称,请画出线段A2B2.
(3)若点P是此平面直角坐标系内的一点,当点A、B1、B2、P四边围成的四边形为平行四边形时,请你直接写出点P的坐标(写出一个即可).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=kx+b(k≠0)和反比例函数y2=
 (m≠0)的图象交于点A(﹣1,6),B(a,﹣2).
(m≠0)的图象交于点A(﹣1,6),B(a,﹣2). 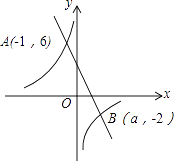
(1)求一次函数与反比例函数的解析式;
(2)根据图象直接写出y1>y2时,x的取值范围. -
科目: 来源: 题型:
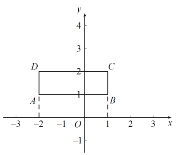
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,长方形ABCD的四个顶点分别为(1,1),(1,2),(-2,2),(-2,1).对该长方形及其内部的每一个点都进行如下操作:把每个点的横坐标都乘以同一个实数a,纵坐标都乘以3,再将得到的点向右平移m(m>0)个单位,向下平移2个单位,得到长方形ABCD及其内部的点,其中点A,B,C,D的对应点分别为A,B,C,D.
(1)点A的横坐标为__________(用含a,m的式子表示).
(2)点A的坐标为(3,1),点C的坐标为(-3,4),
①求a,m的值;
②若对长方形ABCD内部(不包括边界)的点E(0,y)进行上述操作后,得到的对应点E仍然在长方形ABCD内部(不包括边界),求y的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面直角坐标系xOy中的点A,给出如下定义:若存在点B(不与点A重合,且直线AB不与坐标轴平行或重合),过点A作直线m∥x轴,过点B作直线n∥y轴,直线m,n相交于点C.当线段AC,BC的长度相等时,称点B为点A 的等距点,称三角形ABC的面积为点A的等距面积. 例如:如图,点A(2,1),点B(5,4),因为AC= BC=3,所以B为点A 的等距点,此时点A的等距面积为
 .
.(1)点A的坐标是(0,1),在点B1(-1,0),B2(2,3),B3(-1,-1)中,点A 的等距点为________________.
(2)点A的坐标是(-3,1),点A的等距点B在第三象限,
①若点B的坐标是
 ,求此时点A的等距面积;
,求此时点A的等距面积;②若点A的等距面积不小于
 ,求此时点B的横坐标t的取值范围.
,求此时点B的横坐标t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知△ABC是等腰三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.
(1)试猜想线段BG和AE的数量关系;
(2)如图②,将正方形DEFG绕点D按逆时针方向旋转α(0°<α≤90°),判断(1)中的结论是否仍然成立,证明你的结论.

(3)若BC=DE=2,在(2)的旋转过程中,求线段AE长的最大值和最小值
相关试题

