搜索
【题目】如果直角三角形一条直角边长为23，斜边和另一条直角边长的长度都是整数，则这个直角三角形斜边的长为_________________；
参考答案：
【答案】265
【解析】
设这个直角三角形的斜边长为c，另一条直角边长为b.由勾股定理知
，即﹙c－b﹚﹙c＋b﹚＝529＝1×529，又因这个直角三角形的三条边长都是正整数，可得c－b＝1， c＋b＝529，由此即可求得这个直角三角形斜边的长.
设这个直角三角形的斜边长为c，另一条直角边长为b.
由勾股定理知： ，
即﹙c－b﹚﹙c＋b﹚＝529＝1×529
∵ 这个直角三角形的三条边长都是正整数
∴ c－b＝1， c＋b＝529，
解得：c＝265，b＝264.
答：这个直角三角形的斜边长是265.
故答案为：265.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，对角线AC和BD相交于点O，过O作EF⊥AC，交AD于E，交BC于F，连接AF、CE．
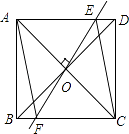
（1）求证：四边形AECF是菱形
（2）若AB=3，BC=4，则菱形AECF的周长？ -
科目： 来源： 题型：
查看答案和解析>>【题目】某玩具厂熟练工人工资为：每月底薪700元，加奖励工资按件计算，一个月工作日为25天，每天工作8小时，加工1件A种玩具计酬10元，加工1件B种玩具计酬8元．在工作中发现一名熟练工人加工1件A种玩具和2件B种玩具需4小时，加工3件A种玩具和1件B种玩具需7小时．（工人月工资=底薪+计件工资）
（1）求熟练工人每加工一件A种玩具和一件B种玩具，分别需要多少时间？
（2）深圳市规定最低工资标准为每月2030元，但玩具厂规定：“每名工人每月必须加工A、B两种工具，且加工A种玩具数量不少于B种玩具的一半”．若设一名熟练工人每月加工A种玩具a件，工资总额为w元，请你运用所学知识判断该公司在执行规定后是否违背了深圳市最低工资标准？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在直角坐标系xoy中，直线l与x、y轴分别交于点A（4，0）、B（0，
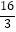）两点，∠BAO的角平分线交y轴于点D．点C为直线l上一点，以AC为直径的⊙G经过点D，且与x轴交于另一点E．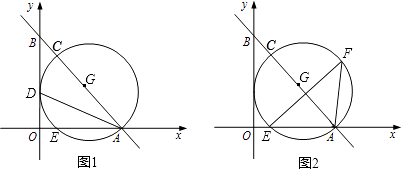 
（1）求证：y轴是⊙G的切线；
（2）请求⊙G的半径r，并直接写出点C的坐标；
（3）如图2，若点F为⊙G上的一点，连接AF，且满足∠FEA=45°，请求出EF的长？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：在△ABC中，∠A、∠B、∠C的对边分别是a、b、c，满足a2+b2+c2+338=10a+24b+26c.
（1）试判断△ABC的形状.
（2）求AB边上的高。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，抛物线l1；y=ax2+bx+c（a＜0）经过原点，与x轴的另一个交点为B（4，0），点A为顶点，且直线OA的解析式为y=x．
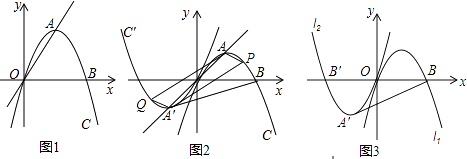
（1）如图1，求抛物线l1的解析式；
（2）如图2，将抛物线l1绕原点O旋转180°，得到抛物线l2 ， l2与x轴交于点B′，顶点为A′，点P为抛物线l1上一动点，连接PO交l2于点Q，连接PA、PA′、QA′、QA．
请求：平行四边形PAQA′的面积S与P点横坐标x（2＜x≤4）之间的关系式；
（3）在（2）的条件下，如图11﹣3，连接BA′，抛物线l1或l2上是否存在一点H，使得HB=HA′？若存在，请求出点H的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】某同学做一道数学题，已知两个多项式A、B，B＝3x2y－5xy＋x＋7，试求A＋B，这位同学把A＋B看成A－B，结果求出的答案为6x2y＋12xy－2x－9．
（1）请你替这位同学求出的正确答案；
（2）当x取任意数值，A－3B的值是一个定值，求y的值．
相关试题
