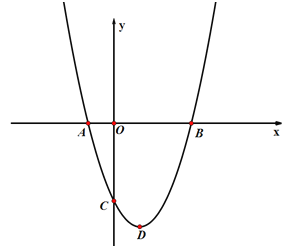
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与
轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与![]() 轴交于点C(0,-3),顶点为D.
轴交于点C(0,-3),顶点为D.
(1)求抛物线的解析式及顶点D的坐标.
(2)联结AC,BC,求∠ACB的正切值.
(3)点P是x轴上一点,是否存在点P使得△PBD与△CAB相似,若存在,请求出点P的坐标;若不存在,请说明理由.
(4)M是抛物线上一点,点N在![]() 轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ,D(1,-4);(2)2;(3)P(
,D(1,-4);(2)2;(3)P(![]() ,0)或P(-3,0);(4)N(1,0)或(
,0)或P(-3,0);(4)N(1,0)或(![]() ,0)或(-3,0).
,0)或(-3,0).
【解析】试题分析:(1)利用待定系数法,把B、C点的坐标代入解析式即可求解;
(2)作AH⊥BC于点H,通过与x轴的交点y=0构成方程,解方程可得A点的坐标,然后解直角三角形可求解;
(3)作DG⊥OB于点G ,tan∠DBG=tan∠ACB,可得∠DBG=∠ACB,然后利用相似三角形的性质和判定讨论得到P点在在点B的左侧,再根据相似三角形的对应边成比例求解即可;
(4)设M点的坐标为(x,x2-2x-3),然后根据A、C点和M的坐标,结合平行四边形的性质与判定求出N点的坐标即可.
试题解析:(1)y=x2-2x-3
D(1,-4)
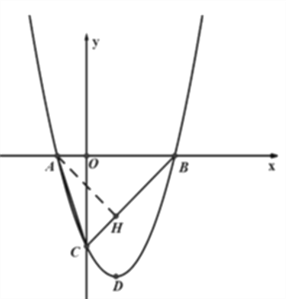
(2)作AH⊥BC于点H
x2-2x-3=0
解得x=-1或x=3
所以A点为(-1,0)
∵ OB=OC,∠BOC=90°
∴∠OBC=45°
∵AB=4
∴AH=BH=2![]()
∵BC=3![]()
∴CH=![]()
∴tan∠ACB=2
(3)作DG⊥OB于点G
∵BG=2,DG=4
∴tan∠DBG=2
∵tan∠ACB=2
∴∠DBG=∠ACB
当点P在点B的右侧时,∠PBD>90°,△PBD是钝角三角形与△CAB不相似,
所以点P在点B的左侧.
∵△PBD与△CAB相似,且∠DBG=∠ACB
∴![]() 或
或![]()
∵BD=2![]()
∴BP=![]() 或BP=6
或BP=6
∴P(-![]() ,0)或P(-3,0)
,0)或P(-3,0)
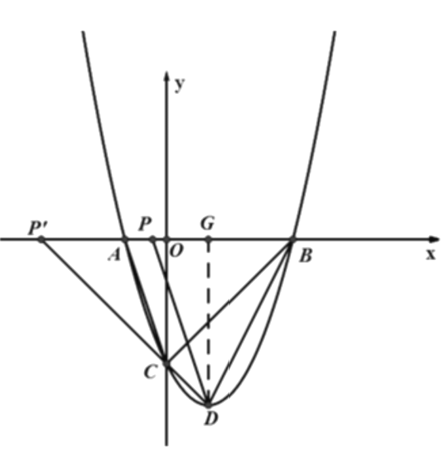
(4)N(1,0)或(![]() ,0)或(-3,0).
,0)或(-3,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若
 ,是
,是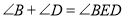 .
.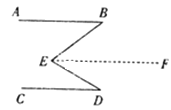
理由:如图,过点
 作
作 ,
,则
 .(依据)
.(依据)因为
 ,
,所以
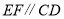 ,
,所以
 .
.所以
 .
.(1)上述证明过程中的依据是指 .
(2)若将点
 移至图2所示的位置,
移至图2所示的位置, ,此时
,此时 之间有什么关系?请说明理由.
之间有什么关系?请说明理由.
(3)在图中,
 ,
, 与
与 又有何关系?
又有何关系?
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:


(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形角平分线交点或三角形内切圆的圆心都称为三角形的内心.按此说法,四边形的四个角平分线交于一点,我们也称为“四边形的内心”.
(1)试举出一个有内心的四边形.
(2)探究:对于任意四边形ABCD,如果有内心,则四边形的边长具备何种条件?为什么?
(3)探究:腰长为
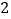 的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?
的等腰直角三角形ABC,∠C=90°,O是△ABC的内心,若沿图中虚线剪开,O仍然是四边形ABDE的内心,此时裁剪线有多少条?(4)问题(3)中,O是四边形ABDE内心,且四边形ABDE是等腰梯形,求DE的长?
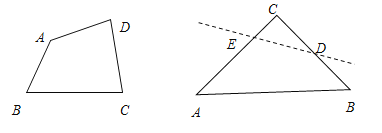
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查,已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
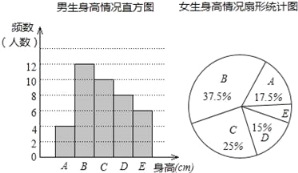
身高情况分组表(单位:cm)
组别
身高
A
x<160
B
160≤x<165
C
165≤x<170
D
170≤x<175
E
x≥175
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组;
(2)样本中,女生身高在E组的人数有 人;
(3)已知该校共有男生600人,女生480人,请估计身高在165≤x<175之间的学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距______千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
(3)B出发后______小时与A相遇.
(4)若B的自行车不发生故障,保持出发时的速度前进,______小时与A相遇,相遇点离B的出发点______千米.在图中表示出这个相遇点C.
(5)求出A行走的路程S与时间t的函数关系式。

-
科目: 来源: 题型:
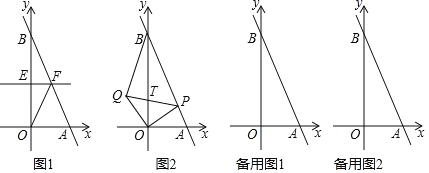
查看答案和解析>>【题目】如图,已知B(0,b)(b>0)是y轴上一动点,直线l经过点A(1,0)及点B,将Rt△ABO折叠,使得点B与点O重合,折痕分别交y轴、直线AB于点E、F,连接OF.
(1)当b=2时,求直线l的函数解析式;
(2)请用含有字母b的代数式表示线段OF的长,并说明线段OF与线段AB的数量关系;
(3)如图,在(1)的条件下,设点P是线段AB上一动点(不与A、B重合),将线段OP绕点O逆时针旋转90°至OQ,连结BQ、PQ,PQ交y轴于点T,设点P的横坐标为t.
①当△OPQ的面积最小时,求T的坐标;
②若△OPB是等腰三角形,请直接写出满足条件的t的值;
③若△OQB是直角三角形,请直接写出满足条件的t的值.
相关试题

