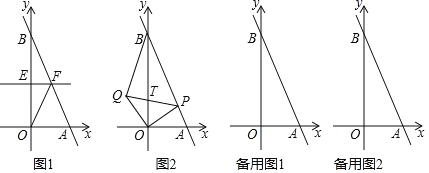
【题目】如图,已知B(0,b)(b>0)是y轴上一动点,直线l经过点A(1,0)及点B,将Rt△ABO折叠,使得点B与点O重合,折痕分别交y轴、直线AB于点E、F,连接OF.
(1)当b=2时,求直线l的函数解析式;
(2)请用含有字母b的代数式表示线段OF的长,并说明线段OF与线段AB的数量关系;
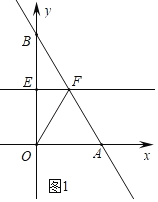
(3)如图,在(1)的条件下,设点P是线段AB上一动点(不与A、B重合),将线段OP绕点O逆时针旋转90°至OQ,连结BQ、PQ,PQ交y轴于点T,设点P的横坐标为t.
①当△OPQ的面积最小时,求T的坐标;
②若△OPB是等腰三角形,请直接写出满足条件的t的值;
③若△OQB是直角三角形,请直接写出满足条件的t的值.
参考答案:
【答案】(1)y=﹣2x+2;(2)OF=![]() ,OF=
,OF=![]() AB,见解析;(3)①T(0,
AB,见解析;(3)①T(0,![]() ),②t的值为
),②t的值为![]() 或
或![]() ,③t的值为1﹣
,③t的值为1﹣![]() .
.
【解析】
(1)利用待定系数法即可解决问题;
(2)利用勾股定理求出AB,利用直角三角形斜边中线的性质即可解决问题;
(3)①根据垂线段最短可知,当OP⊥AB时,△OPQ的面积最小,求出P,Q的坐标,求出直线PQ的解析式即可解决问题;②分两种情形分别求解即可解决问题;③如图5中,取OB的中点G,连接BG.设P(t,-2t+2),求出点Q坐标,根据QG=1构建方程即可解决问题.
(1)如图1中,
由题意A(1,0),B(0,2),设直线AB的解析式为y=kx+b,则有![]() ,
,
解得![]() ,
,
∴直线l的解析式为y=﹣2x+2;
(2)如图1中,∵OB=b,OA=1,
∴AB=![]() ,
,
∵EF垂直平分线段BO,
∴BF=FO,
∵EF∥OA,
∴BF=AF,
∴OF=![]() AB=
AB=![]() ;
;
(3)①如图2中,作PE⊥x轴于E,QF⊥x轴于F.
∵△POQ是等腰直角三角形,
∴当OP的值最小时,△POQ的面积最小,
根据垂线段最短可知,当OP⊥AB时,△OPQ的面积最小,
∵直线OP的解析式为y=![]() x,
x,
由 ,
,
解得![]() ,
,
∴P(![]() ,
,![]() ),
),
∴OE=![]() ,PE=
,PE=![]() ,
,
∵∠PEO=∠QFO=∠POQ=90°,
∴∠POE+∠QOF=90°,∠POE+∠OPE=90°,
∴∠QOF=∠OPE,
∵OP=OQ,
∴△OEP≌△QFO(AAS),
∴QF=OE=![]() ,OF=PE=
,OF=PE=![]() ,
,
∴Q(﹣![]() ,
,![]() ),
),
∴直线PQ的解析式为y=﹣![]() x+
x+![]() ,
,
∴T(0,![]() );
);
②如图3中,当BP=OB=2时,作PE⊥OA于E.
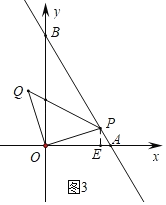
∵PE∥OB,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴PE=![]() ,AE=
,AE=![]() ,
,
∴OE=1﹣![]() =
=![]() .
.
∴t=![]() .
.
如图4中,当PB=PA时,OP=PB满足条件,此时t=![]() .
.
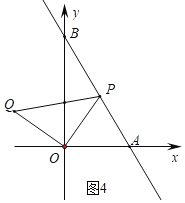
综上所述,满足条件的t的值为![]() 或
或![]() ;
;
③如图5中,取OB的中点G,连接BG.设P(t,﹣2t+2),
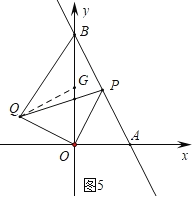
易知Q(2t﹣2,t),G(0,1)当∠OQB=90°时,
∵GB=OG,
∴QG=![]() OB=1,
OB=1,
∴(2t﹣2)2+(t﹣1)2=1,
解得t=1﹣![]() 或1+
或1+![]() (舍弃),
(舍弃),
∴满足条件的t的值为1﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线
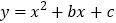 与
与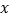 轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与
轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与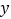 轴交于点C(0,-3),顶点为D.
轴交于点C(0,-3),顶点为D.(1)求抛物线的解析式及顶点D的坐标.
(2)联结AC,BC,求∠ACB的正切值.
(3)点P是x轴上一点,是否存在点P使得△PBD与△CAB相似,若存在,请求出点P的坐标;若不存在,请说明理由.
(4)M是抛物线上一点,点N在
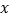 轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.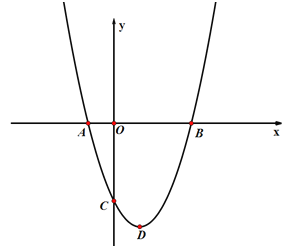
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查,已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
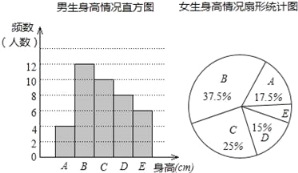
身高情况分组表(单位:cm)
组别
身高
A
x<160
B
160≤x<165
C
165≤x<170
D
170≤x<175
E
x≥175
根据图表提供的信息,回答下列问题:
(1)样本中,男生的身高众数在 组,中位数在 组;
(2)样本中,女生身高在E组的人数有 人;
(3)已知该校共有男生600人,女生480人,请估计身高在165≤x<175之间的学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距______千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
(3)B出发后______小时与A相遇.
(4)若B的自行车不发生故障,保持出发时的速度前进,______小时与A相遇,相遇点离B的出发点______千米.在图中表示出这个相遇点C.
(5)求出A行走的路程S与时间t的函数关系式。

-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽为了测旗杆AB的高度,小丽眼睛距地图1.5米,小丽站在C点,测出旗杆A的仰角为30o,小丽向前走了10米到达点E,此时的仰角为60o,求旗杆的高度。
-
科目: 来源: 题型:
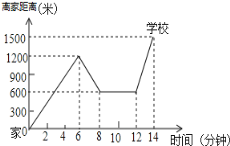
查看答案和解析>>【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米;
(2)小明在书店停留了多少分钟;
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
-
科目: 来源: 题型:
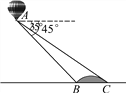
查看答案和解析>>【题目】小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.
(结果保留整数,参考数据:sin35°≈
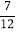 ,cos35°≈
,cos35°≈ ,tan35°≈
,tan35°≈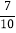 )
)
相关试题

