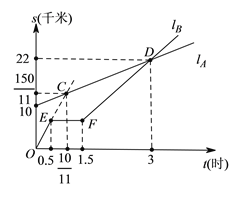
【题目】如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距______千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
(3)B出发后______小时与A相遇.
(4)若B的自行车不发生故障,保持出发时的速度前进,______小时与A相遇,相遇点离B的出发点______千米.在图中表示出这个相遇点C.
(5)求出A行走的路程S与时间t的函数关系式。

参考答案:
【答案】(1)10;(2)1;(3)3;(4)![]() ,
, ![]() ;(5)S=4t+10.
;(5)S=4t+10.
【解析】试题分析:
(1)由图可知,B出发时与A相距10km;
(2)由图可知,B修自行车所用时间为:1.5-0.5=1(小时);
(3)由图象可知,B在出发后3小时的时候与A相遇;
(4)分别求出![]() 的函数关系式和
的函数关系式和![]() 在修车前的函数关系式,由两个解析式组成方程组,解方程组,即可求得所求答案.
在修车前的函数关系式,由两个解析式组成方程组,解方程组,即可求得所求答案.
试题解析:
(1)由图和题意可得:B出发时与A相距10千米.
故答案为:10;
(2)由图和题意可得:修理自行车的时间为:1.5-05=1(小时).
故答案为:1;
(3)由图象可得:B出发3小时时和A相遇,
故答案为:3;
(4)设lA的解析式为:S1=at+b,
∵lA过点(0,10)和(3,22),
∴![]() ,
,
解得: ![]() ,
,
∴S1=4t+10,
设B修车前的关系式为:S2=kt,
∵修车前lB过(0.5,7.5)点.
∴7.5=0.5k,解得:k=15,
∴S2=15t,
由![]() ,解得:
,解得: 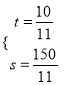 ,
,
即若B的自行车不发生故障,保持出发时的速度前进,则![]() 小时时相遇,此时B走的路程是
小时时相遇,此时B走的路程是![]() 千米.在图中用点C表示相遇点如下图所示:
千米.在图中用点C表示相遇点如下图所示:
(5)由(4)得:A行走的路程S与时间t的函数关系式为:S=4t+10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=-x+m的图象和y轴交于点B,与正比例函数y=x图象交于点P (2,n).
(1)求m和n的值;
(2)求△POB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别交于C,D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,
点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________;
(2)试找出∠1,∠2,∠3之间的等量关系,并说明理由;
(3)应用(2)中的结论解答下列问题;
如图②,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数;
(4)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的关系(点P和A,B两点不重合),直接写出结论即可.



-
科目: 来源: 题型:
查看答案和解析>>【题目】某兴趣小组为了了解本校学生参加课外体育锻炼情况,随机抽取本校40名学生进行问卷调查,统计整理并绘制了如下两幅尚不完整的统计图:

根据以上信息解答下列问题:
(1)课外体育锻炼情况统计图中,“经常参加”所对应的圆心角的度数为 ;“经常参加课外体育锻炼的学生最喜欢的一种项目”中,喜欢足球的人数有 人,补全条形统计图.
(2)该校共有1200名学生,请估计全校学生中经常参加课外体育锻炼并喜欢的项目是乒乓球的人数有多少人?
(3)若在“乒乓球”、“篮球”、“足球”、“羽毛球”项目中任选两个项目成立兴趣小组,请用列表法或画树状图的方法求恰好选中“乒乓球”、“篮球”这两个项目的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个只含有两个字母,且次数为3的单项式_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠D=∠C=90°,E是DC的中点,AE平分∠DAB,∠DEA=28°,则∠ABE的度数是( )
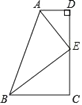
A. 62° B. 31° C. 28° D. 25°
相关试题

