【题目】常常听说“勾3股4弦5”,是什么意思呢?它就是勾股定理,即“直角三角形两直角边长a,b与斜边长c之间满足等式:a2+b2=c2”的一个最简单特例.我们把满足a2+b2=c2的三个正整数a,b,c,称为勾股数组,记为(a,b,c).
(1)请在下面的勾股数组表中写出m、n、p合适的数值:
a | b | c | a | b | c |
3 | 4 | 5 | 4 | 3 | 5 |
5 | 12 | m | 6 | 8 | 10 |
7 | 24 | 25 | p | 15 | 17 |
9 | n | 41 | 10 | 24 | 26 |
11 | 60 | 61 | 12 | 35 | 37 |
… | … | … | … | … | … |
平面直角坐标系中,横、纵坐标均为整数的点叫做整点(格点).过x轴上的整点作y轴的平行线,过y轴上的整点作x轴的平行线,组成的图形叫做正方形网格(有时简称网格),这些平行线叫做格边,当一条线段AB的两端点是格边上的点时,称为AB在格边上.顶点均在格点上的多边形叫做格点多边形.在正方形网格中,我们可以利用勾股定理研究关于图形面积、周长的问题,其中利用割补法、作图法求面积非常有趣.
(2)已知△ABC三边长度为4、13、15,请在下面的网格中画出格点△ABC并计算其面积.

参考答案:
【答案】(1)m=13,n=40,p=8;(2)图详见解析,24.
【解析】
(1)根据勾股数的定义计算即可;
(2)根据勾股数确定长为13和15的边,再根据三角形的面积公式计算即可.
(1)根据勾股数的定义计算即可;
(2)根据勾股数确定长为13和15的边,再根据三角形的面积公式计算即可.
解:(1)∵52+122=132,
∴m=13;
∵92+402=412,
∴n=40,
∵82+152=172,
∴p=8.
(2)如图所示:
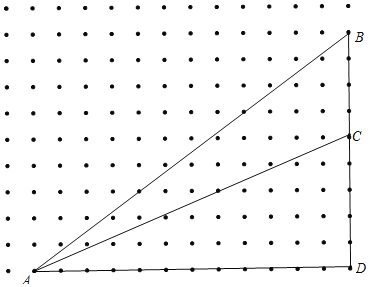
在△ABC中,AB=15,BC=4,AC=13,
S△ABC=SABD﹣S△ACD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程
已知:直线l及直线l外一点P.

求作:直线PQ,使得PQ∥l.
作法:如图,

①在直线l上取一点A,作射线AP,以点P为圆心,PA长为半径画弧,交AP的
延长线于点B;
②以点B为圆心,BA长为半径画弧,交l于点C(不与点A重合),连接BC;
③以点B为圆心,BP长为半径画孤,交BC于点Q;
④作直线PQ.
所以直线PQ就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明
证明:∵PB=PA,BC= ,BQ=PB,
∴PB=PA=BQ= .
∴PQ∥l( )(填推理的依据).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小丁设计的“利用直角三角形和它的斜边中点作矩形”的尺规作图过程.
已知:如图,在RtΔABC中,∠ABC=90°,0为AC的中点.
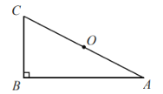
求作:四边形ABCD,使得四边形ABCD为矩形.
作法:①作射线BO,在线段BO的延长线上取点D,使得DO=BO;
②连接AD,CD,则四边形ABCD为矩形.
根据小丁设计的尺规作图过程.
(1)使用直尺和圆规,在图中补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∴点O为AC的中点,
∴AO=CO.
又∵DO=BO,
∵四边形ABCD为平行四边形(__________)(填推理的依据).
∵∠ABC=90°,
∴
 ABCD为矩形(_________)(填推理的依据).
ABCD为矩形(_________)(填推理的依据). -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;②b+c=0;③2b+c+3=0;④当1<x<3时,x2+(b﹣1)x+c<0
其中正确的有( )个.

A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .

-
科目: 来源: 题型:
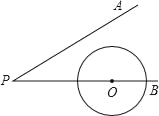
查看答案和解析>>【题目】如图,∠APB=30°,圆心在PB上的⊙O的半径为1cm,OP=3cm,若⊙O沿BP方向平移,当⊙O与PA相切时,圆心O平移的距离为_____cm.
-
科目: 来源: 题型:
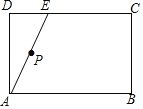
查看答案和解析>>【题目】如图,矩形ABCD中,点E为矩形的边CD上的任意一点,点P为线段AE的中点,连接BP并延长与边AD交于点F,点M为边CD上的一点,且CM=DE,连接FM.
(1)依题意补全图形;
(2)求证∠DMF=∠ABF.
相关试题

