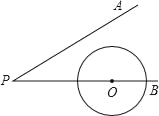
【题目】如图,∠APB=30°,圆心在PB上的⊙O的半径为1cm,OP=3cm,若⊙O沿BP方向平移,当⊙O与PA相切时,圆心O平移的距离为_____cm.
参考答案:
【答案】1或5
【解析】试题分析:首先根据题意画出图形,然后由切线的性质,可得∠O′CP=90°,又由∠APB=30°,O′C=1cm,即可求得O′P的长,继而求得答案.
解:有两种情况:
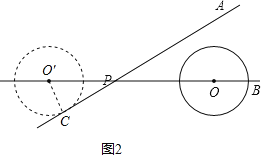
(1)如图1,当O平移到O′位置时,O与PA相切时,且切点为C,
连接O′C,则O′C⊥PA,即∠O′CP=90°,

∵∠APB=30°,O′C=1cm,
∴O′P=2O′C=2cm,
∵OP=3cm,
∴OO′=OPO′P=1(cm).
(2)如图2,同理可得:O′P=2cm,
∴O′O=5cm.
故答案为:1或5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;②b+c=0;③2b+c+3=0;④当1<x<3时,x2+(b﹣1)x+c<0
其中正确的有( )个.

A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】常常听说“勾3股4弦5”,是什么意思呢?它就是勾股定理,即“直角三角形两直角边长a,b与斜边长c之间满足等式:a2+b2=c2”的一个最简单特例.我们把满足a2+b2=c2的三个正整数a,b,c,称为勾股数组,记为(a,b,c).
(1)请在下面的勾股数组表中写出m、n、p合适的数值:
a
b
c
a
b
c
3
4
5
4
3
5
5
12
m
6
8
10
7
24
25
p
15
17
9
n
41
10
24
26
11
60
61
12
35
37
…
…
…
…
…
…
平面直角坐标系中,横、纵坐标均为整数的点叫做整点(格点).过x轴上的整点作y轴的平行线,过y轴上的整点作x轴的平行线,组成的图形叫做正方形网格(有时简称网格),这些平行线叫做格边,当一条线段AB的两端点是格边上的点时,称为AB在格边上.顶点均在格点上的多边形叫做格点多边形.在正方形网格中,我们可以利用勾股定理研究关于图形面积、周长的问题,其中利用割补法、作图法求面积非常有趣.
(2)已知△ABC三边长度为4、13、15,请在下面的网格中画出格点△ABC并计算其面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .

-
科目: 来源: 题型:
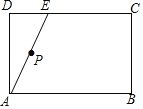
查看答案和解析>>【题目】如图,矩形ABCD中,点E为矩形的边CD上的任意一点,点P为线段AE的中点,连接BP并延长与边AD交于点F,点M为边CD上的一点,且CM=DE,连接FM.
(1)依题意补全图形;
(2)求证∠DMF=∠ABF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)小My同学在网络直播课中学习了勾股定理,他想把这一知识应用在等边三角形中:边长为a的等边三角形面积是 (用含a的代数式表示);
(2)小My同学进一步思考:是否可以将正方形剪拼成一个等边三角形(不重叠、无缝隙)?
①如果将一个边长为2的正方形纸片剪拼等边三角形,那么该三角形边长的平方是 ;
②小My同学按下图切割方法将正方形ABCD剪拼成一个等边三角形EFG:M、N分别为AB、CD边上的中点,P、Q是边BC、AD上两点,G为MQ上一点,且∠MGP=∠PGN=∠NGQ=60°.
请补全图形,画出拼成正三角形的各部分分割线,并标号;
③正方形ABCD的边长为2,设BP=x,则x2= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,双边直尺有两条平行的边,但是没有刻度,可以用来画等距平行线:

我们也可用工具自制(如图):

下面是小My同学设计的“过直线外一点作这条直线的平行线”的双边直尺作图过程.
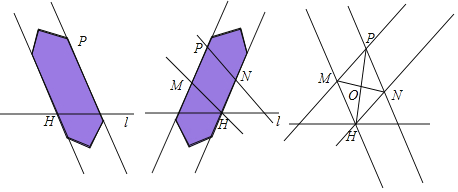
(1)根据小My同学的作图过程,请证明O为PH中点.
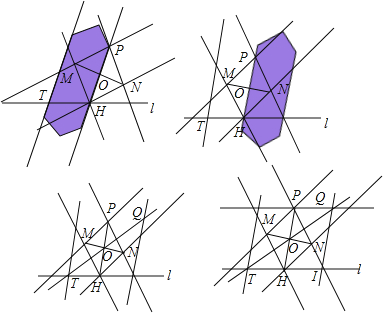
(2)根据小My同学的作图过程,请证明PQ∥l.
相关试题

