【题目】已知∠AOB=50°,过点O引射线OC,若∠AOC:∠BOC=2:3,OD平分∠AOB,求∠COD的度数.

参考答案:
【答案】∠COD=5°或∠COD=125°.
【解析】
分射线OC在∠AOB的内部、射线OC在∠AOB的外部两种情况进行解答,当射线OC在∠AOB的内部时,设∠AOC=2x,则∠COB=3x,计算出x的值,进而计算出∠AOC、∠AOD的度数,从而得出结论.当射线OC在∠AOB的外部时,设∠AOC=2x,则∠COB=3x,则∠AOB=x,得x的值,进而计算出∠AOC与∠AOD的度数,然后得出结论.
分两种情况讨论:
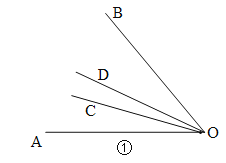
(1)射线OC在∠AOB的内部,如图①;
设∠AOC=2x,则∠COB=3x,则2x+3x=50°,∴x=10°,∠AOC=2x=20°,∠AOD![]() 50°=25°,∴∠COD=∠AOD﹣∠AOC=25°﹣20°=5°;
50°=25°,∴∠COD=∠AOD﹣∠AOC=25°﹣20°=5°;
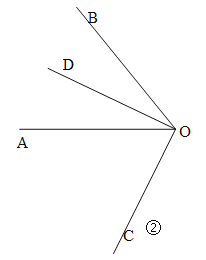
(2)射线OC在∠AOB的外部,如图②.
设∠AOC=2x,则∠COB=3x,则∠AOB=3x﹣2x=x=50°,∴∠AOC=2x=100°
∠AOD=25°,∴∠COD=∠AOC+∠AOD=100°+25°=125°.
综上所述:∠COD=5°或∠COD=125°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,直线
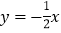 与反比例函数
与反比例函数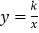 的图象交于A,B两点,已知A点的纵坐标是2.
的图象交于A,B两点,已知A点的纵坐标是2.(1)求反比例函数的解析式.
(2)将直线
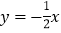 沿x轴向右平移6个单位后,与反比例函数在第二象限内交于点C.动点P在y轴正半轴上运动,当线段PA与线段PC之差达到最大时,求点P的坐标.
沿x轴向右平移6个单位后,与反比例函数在第二象限内交于点C.动点P在y轴正半轴上运动,当线段PA与线段PC之差达到最大时,求点P的坐标.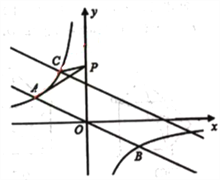
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,小明和小颖两家共8人相约外出旅行,分别乘坐两辆出租车前往机场在距离机场11千米处一辆车出了故障不能继续行驶.此时离机场停止办理登机手续还有30分钟,唯一可以利用的交通工具只有另一辆出租车,连同司机在内限乘5人,车速每小时60千米.
(1)如果这辆车分两批接送,其中4人乘车先走,余下4人原地等候,8人能否及时到达机场办理登机手续?(上下车时间忽略不计)
(2)如果这辆车在送第一批客人的时候,余下的人以每小时6千米的速度步行前往机场,待司机将第一批客人送达后立即返回接第二批客人,他们能及时到达机场吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某初级中学数学兴趣小组为了了解本校学生的年龄情况,随机调查了该校部分学生的年龄,整理数据并绘制如下不完整的统计图.
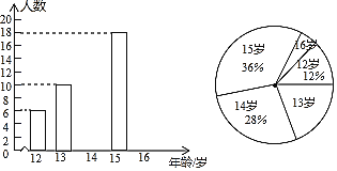
依据以上信息解答以下问题:
(1)分别求出14岁和16岁的学生人数,并补全条形统计图;
(2)这个样本的众数是_____岁,中位数是_____岁;
(3)若该校一共有1800名学生,估计该校年龄在15岁及以上的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商城的智能手机销售异常火爆,若销售10部
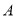 型和20部
型和20部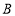 型手机的利润共4000元,每部
型手机的利润共4000元,每部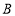 型手机的利润比每部型手机多50元.
型手机的利润比每部型手机多50元.(1)求每部
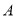 型手机和
型手机和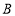 型手机的销售利润.
型手机的销售利润.(2)商城计划一次购进两种型号的手机共100部,其中型手机的进货量不超过
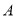 型手机的2倍,则商城购进
型手机的2倍,则商城购进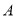 型、
型、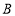 型手机各多少部,才能使销售利润最大?最大利润是多少?
型手机各多少部,才能使销售利润最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(感知)如图①,四边形
 、
、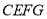 均为正方形.
均为正方形.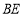 与
与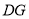 的数量关系为________;
的数量关系为________;(2)(拓展)如图②,四边形
 、
、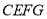 均为菱形,且
均为菱形,且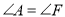 .请判断
.请判断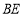 与
与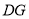 的数量关系,并说明理由;
的数量关系,并说明理由;(3)(应用)如图③,四边形
 、
、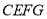 均为菱形,点
均为菱形,点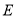 在边
在边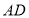 上,点
上,点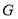 在
在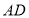 延长线上.若
延长线上.若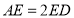 ,
,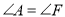 ,
,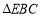 的面积为9,则菱形
的面积为9,则菱形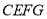 的面积为_______.
的面积为_______.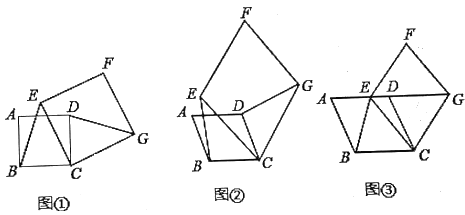
-
科目: 来源: 题型:
查看答案和解析>>【题目】高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.
相关试题

